지붕 표면 열 플럭스가 난류 고유 구조 및 오염물질 분산에 미치는 효과에 대한 큰 에디 모의

1. 서 론

도시 지역에서는 다양한 건물 구조와 도시 지표면의 열적 특성으로 인해 복잡한 흐름이 나타난다 (Yazid et al., 2014; Roth, 2000). 특히 도시 지역에서 발달하는 난류 고유 구조 (turbulent coherent structure)는 열, 바람 환경 및 오염물질 분산에 중요한 역할을 한다. 난류 고유 구조는 반복적으로 나타나는 조직화된 난류 구조를 의미한다 (Fiedler, 1988). 배경 흐름에 나란한 방향으로 길게 발달하는 줄무늬 (streak) 형태의 저속 난류 흐름은 도시 지역에서 나타나는 대표적인 난류 고유 구조 중 하나이다 (Takimoto et al., 2013; Michioka and Sato, 2012; Kanda et al., 2004). 이러한 저속 난류 흐름 근처에서는 헤어핀 형태의 와류가 형성되기도 한다 (Coceal et al., 2007). 한편 건물 지붕 근처에서는 여러 작은 규모의 난류 고유 구조가 발달하며 고도가 증가함에 따라 난류 고유 구조의 수는 감소하지만 그 크기는 증가하는 것으로 알려져 있다 (Michioka et al., 2011; Inagaki and Kanda, 2010; Kanda, 2006). 도시 지역에서 난류 고유 구조의 특성은 건물 형태, 배치, 높이 등에 따라 다르게 나타난다 (Tian et al., 2024; Akinlabi et al., 2022; Yoshida and Takemi, 2021; Park et al., 2015).

지표면 열 플럭스는 난류 고유 구조의 특성에 큰 영향을 미치는 인자 중 하나이다. 도시 지역에서의 난류 고유 구조를 잘 모의할 수 있는 큰 에디 모의 (large-eddy simulation) 모형을 이용하여 지표면 열 플럭스가 난류 고유 구조에 미치는 영향에 대해 다양한 수치 연구가 수행된 바 있다. Inagaki et al. (2012)은 나란하게 정렬된 건물 배열에 대해 도로와 지붕 표면에서 상향 열 플럭스가 존재할 경우 지붕 고도 위에 나타나는 줄무늬 형태의 난류 고유 구조와 지붕 고도 아래의 흐름이 강한 연관성을 보임을 밝혔다. Boppana et al. (2014)은 도로 표면에서 상향 열 플럭스가 증가할 경우 대기가 불안정해짐에 따라 난류 운동 에너지가 증가하며 난류 구조의 연직 크기가 증가함을 보였다. Li et al. (2010)은 2차원 도로 협곡에 대해 도로 표면에서 상향 열 플럭스가 증가할 경우 지붕 고도에서 난류에 의한 오염물질 유출이 증가함을 밝혔다. Park and Baik (2013)은 나란하게 정렬된 건물 배열 (building array)에 대해 도로 표면에서 상향 열 플럭스가 존재할 경우 분출 (ejection) 현상과 2차 순환이 강화되어 오염물질의 연직 확산이 활발해지고 연직 난류 운동량 플럭스의 크기가 증가함을 보였다.

건물 지붕은 건물 벽면과 도로면에 비해 표면 온도의 변화폭이 크며 (Trimmel et al., 2019; Lemonsu et al., 2004), 이로 인해 건물 주변의 난류 고유 구조에 더 큰 영향이 있을 것으로 기대된다. 하지만 지붕 표면 열 플럭스가 난류 고유 구조에 미치는 효과에 대해서는 조사된 바가 상대적으로 적다. 또한 기존 연구들은 주로 지표면에서 상향 열 플럭스가 나타날 때의 난류 고유 구조 및 오염물질 분산 특성만을 조사하였으며, 도시 지표면이 냉각되어 하향 열 플럭스가 나타날 경우의 난류 고유 구조 및 오염물질 분산 특성은 충분히 조사되지 않았다. 따라서 본 연구에서는 건물 지붕에서의 상향 및 하향 열 플럭스가 건물 주변에서의 난류 고유 구조에 미치는 영향을 상세히 조사하고자 한다. 또한 건물 지붕 표면 열 플럭스에 의한 난류 고유 구조의 변화가 오염물질 분산에 어떠한 영향을 미치는지 탐구하고자 한다.

2. 수치 모형 및 실험 설계

본 연구에서 이용한 큰 에디 모의 모형은 PALM (PArallelized Large-eddy simulation Model) 6.0 버전 (Maronga et al., 2020)이다. PALM은 부시네스크 근사가 적용된 여과된 (filtered) 비정수 나비어-스톡스 방정식을 지배 방정식으로 사용하며, 수정된 1.5차 디어도르프 난류 종결 방법을 아격자 규모 난류 모수화 방안으로 사용한다 (Saiki et al., 2000; Moeng and Wyngaard, 1988; Deardorff, 1980). PALM은 시간 차분법으로 3차 룽게-쿠타 방법을, 공간 차분법으로 5차 풍상차분법을 사용하며, 격자계로 아라카와 C 격자계를 사용한다. PALM은 매 적분마다 쿠랑-프리데리흐스-레위 (Courant-Friedrichs-Lewy) 조건을 만족하는 최대 시간 간격을 적분 시간 간격으로 사용한다. PALM은 모닌-오브코프 상사 이론을 이용하여 건물 표면과 도로 표면의 운동량 플럭스와 열 플럭스를 계산한다. PALM은 도시에서의 흐름 및 난류 연구에 활발히 사용되고 있으며 (Duan et al., 2023; Lo and Ngan, 2015; Park and Baik, 2013; Inagaki et al., 2012), 관측 및 풍동 실험 결과를 잘 모의한다 (An and Park., 2024; Du et al., 2024; Belda et al., 2021; Resler et al., 2021). PALM에 관한 보다 상세한 정보는 Maronga et al. (2020)에 기술되어 있다.

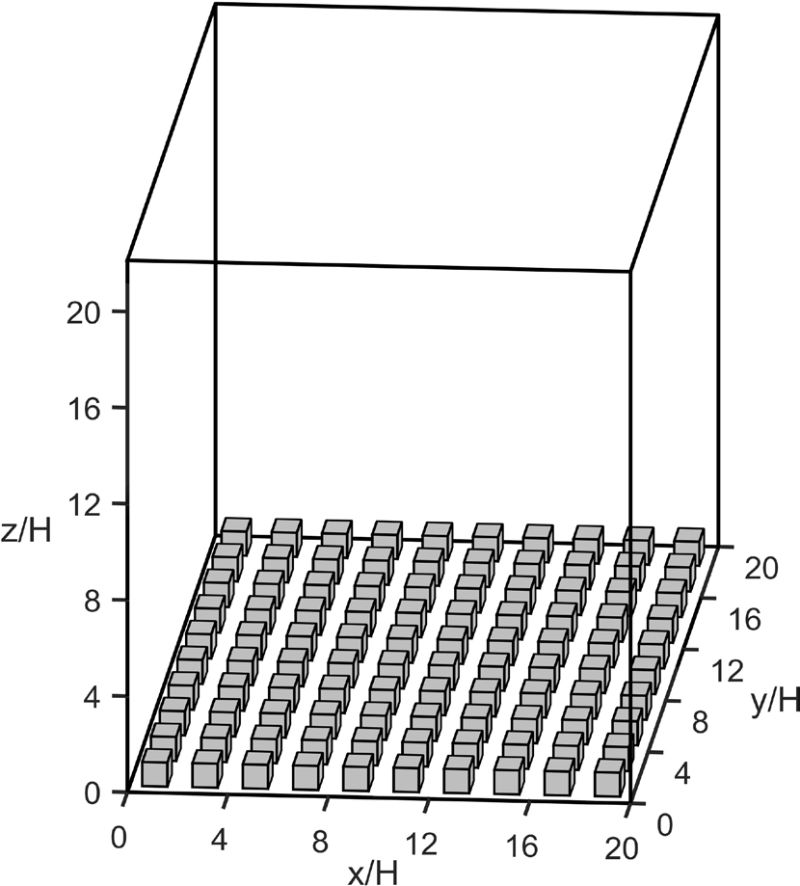
본 연구에서는 10 (x 방향)×10 (y 방향)개의 건물을 고려하였다 (그림 1). 건물은 높이 (H)와 너비가 32 m로 동일한 정육면체 형태이며, 건물 사이의 간격 또한 32 m로 설정하였다. 계산 영역의 크기는 x, y, z 방향으로 각각 640, 640, 708 m이다. 수평 격자 간격은 0.5 m이다. 연직 격자 간격은 고도 200 m 이하와 298 m 이상에서 각각 2, 10 m로 일정하며, 고도 200 m와 고도 298 m 사이에서는 격자 간격이 2 m에서 10 m에 도달할 때까지 1.08배씩 점진적으로 증가하도록 설정하였다. 초기 풍속은 모든 격자점에서 8 m s^-1로 일정하며, 초기 풍향은 모든 격자점에서 양의 x 방향이다. 초기 온위는 모든 격자점에서 300 K이다. 초기 오염물질 농도는 모든 격자점에서 0 μg m^-3이며, 이후 도로의 모든 격자점에서 1 μg m^-2 s^-1의 일정한 배출율로 배출된다. 속도 성분, 온위, 오염물질 농도 등을 포함한 예단 변수에 대해 수평 방향에 대해서는 주기 경계 조건을, 연직 방향 최상단 경계에서는 노이만 경계 조건을 사용하였다.

Fig. 1.

Computational domain and a building array. H represents the building height.

지붕 표면 열 플럭스가 난류 고유 구조와 오염물질 분산에 미치는 영향을 조사하기 위해 총 세 가지 실험을 수행하였다. 먼저 규준 실험에서는 표면 열 플럭스가 없는 중립 대기 상태를 고려하였으며, 중립 실험으로 명명하였다. 나머지 두 실험에서는 지붕 표면의 모든 격자점에서 0.1 K m s^-1로 일정한 상향, 하향 열 플럭스를 고려하였으며 이는 각각 지붕 표면이 가열된 경우, 냉각된 경우에 해당한다. 이러한 이유로 두 실험을 각각 가열 실험, 냉각 실험으로 명명하였다. 각 실험의 적분 기간은 총 2시간이며, 마지막 30분의 모의 자료를 분석에 이용하였다. 세 실험에서 모두 적분 기간 동안 적분 시간 간격은 0.2초 미만이며, 이는 건물 주변의 난류 고유 구조를 모의하기에 충분히 짧다.

3. 결과 및 고찰

3. 1 연직 프로파일

그림 2는 중립 실험, 가열 실험, 냉각 실험에서 수평 방향과 시간에 대해 평균한 x 방향 속도, 오염물질 농도, 온위, 난류 운동 에너지, 연직 속도 분산, 연직 난류 운동량 플럭스, 연직 난류 오염물질 플럭스, 연직 난류 열 플럭스의 연직 프로파일을 보여준다. u는 x 방향 속도를, w는 연직 속도를, c는 오염물질 농도를, θ는 온위를 의미한다. 오버바 ( · )는 시간 평균을, 꺾쇠괄호 (<·>)는 특정 고도에서의 수평 평균을, 작은따옴표 (·ʹ)는 수평 평균으로부터의 편차를 의미한다 (An and Park, 2024; Han et al., 2019).

Fig. 2.

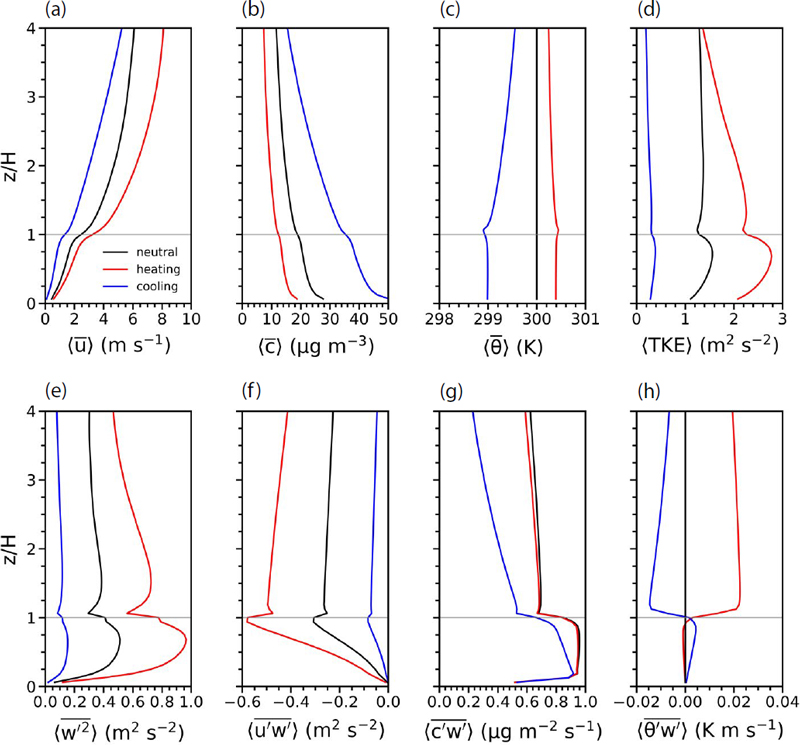
Spatially and temporally averaged vertical profiles of (a) streamwise velocity, (b) pollutant concentration, (c) potential temperature, (d) resolved turbulent kinetic energy, (e) resolved vertical velocity variance, (f) resolved vertical turbulent momentum flux, (g) resolved vertical pollutant flux, and (h) resolved vertical heat flux in the neutral (black), heating (red), and cooling (blue) simulations. The roof level (z/H=1) is denoted by the gray horizontal line.

x 방향 흐름은 중립 실험에 비해 가열 실험에서 더 강하게 나타났으며 냉각 실험에서는 더 약하게 나타났다 (그림 2(a)). 지붕 고도에서의 x 방향 속도는 중립 실험에서 2.45 m s^-1이며, 가열 실험과 냉각 실험에서 각각 3.25, 1.34 m s^-1이다. 평균 흐름이 강해짐에 따라 평균 오염물질 농도는 감소한다 (그림 2(b)). 보행자 고도 근처 (z/H=0.0625)에서 평균 오염물질 농도는 냉각 실험, 중립 실험, 가열 실험에서 각각 50.3, 27.8, 18.8 μg m^-3로 나타났다. 중립 실험 대비 가열 실험에서의 평균 온위 증가와 냉각 실험에서의 평균 온위 감소는 지붕 고도 약간 위에서 가장 뚜렷하다 (그림 2(c)). 가열 실험에서 최대 온위는 z/H=1.0625에서 300.45 K이며 냉각 실험에서 최소 온위는 z/H=1.0625에서 298.90 K이다. 가열 실험에서는 z/H=1.0625 위에서 온위가 고도에 따라 감소하여 정적 불안정이 나타나며, 냉각 실험에서는 z/H=1.0625 위에서 온위가 고도에 따라 증가하여 정적 안정이 나타난다. 한편 가열 실험에서는 지붕 고도 바로 아래에서 정적 안정이 나타나며, 냉각 실험에서는 지붕 고도 바로 아래에서 정적 불안정이 나타난다. 동일한 크기의 열 플럭스를 고려하였음에도 불구하고 z/H=4 이하에서 중립 실험 대비 온위 변화는 가열 실험에서가 냉각 실험에서보다 뚜렷이 작다. 이는 가열 실험에서는 지붕 고도 위에서 정적 불안정이 나타나 지붕 고도 근처의 가열된 공기가 난류에 의해 상대적으로 넓은 고도 범위에서 활발히 혼합된 반면, 냉각 실험에서는 지붕 고도 위에서 정적 안정이 나타나 지붕 고도 근처의 냉각된 공기가 상대적으로 제한된 고도 범위에서 혼합되었기 때문이다. 난류 운동 에너지는 중립 실험 대비 가열 실험에서 증가, 냉각 실험에서 감소하였으며, 지붕 고도 위에서보다 지붕 고도 아래에서 그 변화가 상대적으로 뚜렷하다 (그림 2(d)). 최대 난류 운동 에너지는 가열 실험과 중립 실험에서는 z/H=0.6875, 냉각 실험에서는 z/H=0.75에서 나타나며, 가열 실험, 중립 실험, 냉각 실험에서 각각 2.78, 1.56, 0.39 m² s^-2로 실험 간 차이가 뚜렷하다. 지붕 고도 아래에서 평균한 난류 운동 에너지는 중립 실험 대비 가열 실험에서 79.6% 증가하였으며 중립 실험 대비 냉각 실험에서 75.6% 감소하였다.

중립 실험 대비 가열 실험, 냉각 실험에서의 연직 속도 분산의 변화는 난류 운동 에너지의 변화와 매우 유사한 형태로 나타난다 (그림 2(e)). 연직 난류 운동량 플럭스는 세 실험에서 모두 하향으로 나타나며, 그 크기는 가열 실험, 중립 실험, 냉각 실험 순으로 크다 (그림 2(f)). 이는 가열 실험에서 중립 실험 대비 난류 운동이 강화됨에 따라 연직 난류 운동량 수송이 강화되었으며, 냉각 실험에서 중립 실험 대비 난류 운동이 약화됨에 따라 연직 난류 운동량 수송이 약화되었음을 의미한다. 최대 하향 연직 난류 운동량 플럭스는 세 실험에서 모두 지붕 고도 약간 아래에서 나타난다. 연직 난류 오염물질 플럭스는 세 실험에서 모두 상향으로 나타나며, 최대 크기는 지붕 고도 아래에서 나타난다 (그림 2(g)). 연직 난류 오염물질 플럭스의 크기는 중립 실험과 가열 실험에서 전반적으로 유사한 반면, 냉각 실험에서의 연직 난류 오염물질 플럭스의 크기는 두 실험에서보다 전반적으로 더 낮다. 가열 실험에서는 중립 실험 대비 난류 운동이 강화되었음에도 연직 난류 오염물질 플럭스의 크기가 유사하게 나타났는데, 이는 오염물질의 연직 혼합이 강화되어 지붕 고도 근처에서 오염물질 농도의 연직 경도가 감소한 것과 관련이 있다. 연직 난류 열 플럭스는 가열 실험에서는 지붕 고도 아래에서 하향, 지붕 고도 위에서 상향으로 나타나며, 냉각 실험에서는 지붕 고도 아래에서 상향, 지붕 고도 위에서 하향으로 나타난다 (그림 2(h)). 연직 난류 열 플럭스의 크기는 지붕 고도 아래에서는 가열 실험에서보다 냉각 실험에서 전반적으로 더 큰 반면, 지붕 고도 위에서는 냉각 실험에서보다 가열 실험에서 전반적으로 더 크다. 이는 지붕 고도 위에서는 가열 실험에서가 냉각 실험에서보다 대기가 불안정하여 난류에 의한 열 에너지 교환이 더 활발하고, 지붕 고도 바로 아래에서는 냉각 실험에서가 가열 실험에서보다 대기가 불안정해 난류에 의한 열 에너지 교환이 더 활발하기 때문이다.

3. 2 난류 고유 구조

그림 3은 중립 실험, 가열 실험, 냉각 실험에서 t=7200초일 때 보행자 고도 근처, 지붕 고도, 상층 고도 (z/H=2)에서의 정규화된 x 방향 속도 편차의 수평 분포를 보여준다. x 방향 속도 편차는 x 방향 속도의 표준 편차로 나누어 정규화하였다. 그림 3에 빨간색과 파란색으로 나타난 영역은 정규화된 값이 각각 +1 이상, -1 이하인 영역을 의미한다. 중립 실험에서 세 고도에서의 x 방향 속도 편차는 서로 유사한 분포를 보이며, 주로 x 방향으로 길게 발달한 줄무늬 형태의 난류 고유 구조가 나타난다 (그림 3(a), 3(b)와 3(c)). 분석 기간 동안 보행자 고도 근처에서의 x 방향 속도 편차와 지붕 고도에서의 x 방향 속도 편차, 지붕 고도에서의 x 방향 속도 편차와 상층 고도에서의 x 방향 속도 편차 간의 피어슨 상관 계수는 각각 0.43, 0.49로 통계적으로 유의하다 (p<0.01).

Fig. 3.

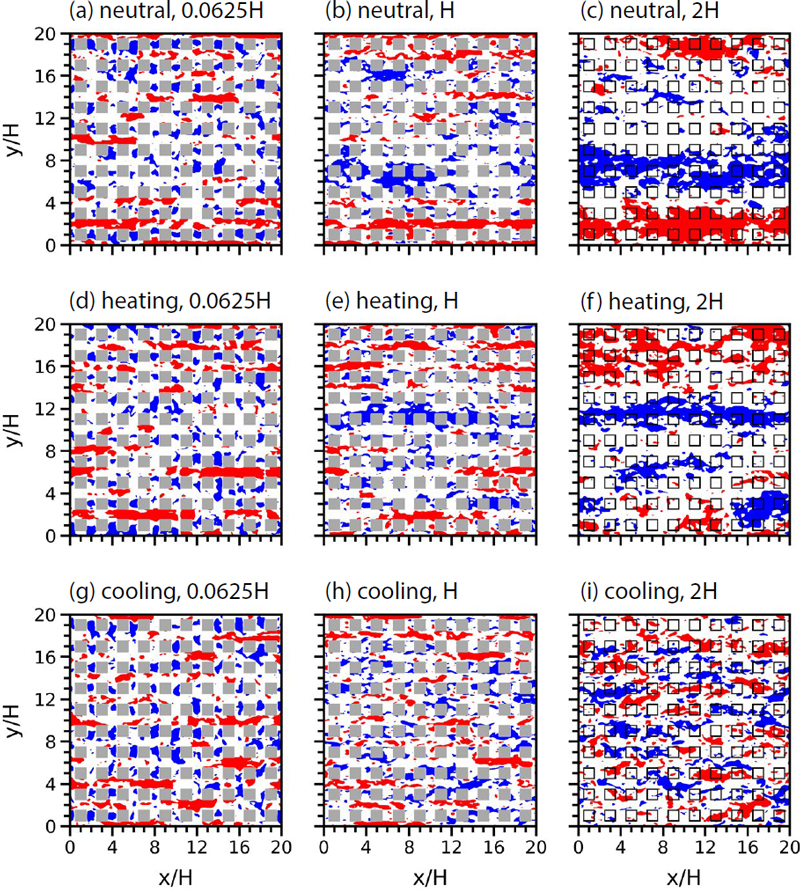
Fields of normalized streamwise velocity deviation at z/H=(a, d, g) 0.0625, (b, e, h) 1, and (c, f, i) 2 at t=7200 s in the (a, b, c) neutral, (d, e, f) heating, and (g, h, i) cooling simulations. The normalized streamwise velocity deviations larger than 1 and smaller than -1 are indicated by the red and blue shaded areas, respectively.

가열 실험에서는 중립 실험에서와 비슷하게 x 방향 속도 편차의 분포가 세 고도에서 유사하며, 주로 x 방향으로 발달한 난류 고유 구조가 나타난다 (그림 3(d), 3(e)와 3(f)). 가열 실험에서 분석 기간 동안 보행자 고도 근처에서의 x 방향 속도 편차와 지붕 고도에서의 x 방향 속도 편차, 지붕 고도에서의 x 방향 속도 편차와 상층 고도에서의 x 방향 속도 편차 간의 피어슨 상관 계수는 각각 0.43, 0.41로 통계적으로 유의하다 (p< 0.01). 냉각 실험에서 보행자 고도 근처에서와 지붕 고도에서의 x 방향 속도 편차 분포는 일부 유사성을 보이며 (그림 3(g)와 3(h)), 분석 기간 동안 두 고도에서의 x 방향 속도 편차 간의 피어슨 상관 계수는 0.34로 통계적으로 유의하나 (p<0.01) 중립 실험 및 가열 실험에서에 비해 더 낮다. 반면 상층 고도에서의 x 방향 속도 편차 분포는 보행자 고도 근처 및 지붕 고도에서와 뚜렷하게 다르며 (그림 3(i)), 분석 기간 동안 지붕 고도에서의 x 방향 속도 편차와 상층 고도에서의 x 방향 속도 편차 간의 피어슨 상관 계수는 0.13으로 상관성이 잘 나타나지 않는다. 또한 냉각 실험에서 상층 고도의 난류 고유 구조의 크기는 다른 두 실험에서에 비해 뚜렷이 작다. 따라서 이러한 결과는 지붕 표면이 냉각되어 대기가 안정해질 경우 상·하층의 난류 고유 구조 간 연관성이 매우 낮아짐을 의미한다.

세 실험 간 난류 고유 구조의 차이를 더 상세히 비교하고자 t=7200초일 때 x/H=10에서의 x 방향 속도 편차의 연직 단면을 비교하였다 (그림 4). 양의 x 방향 속도 편차는 주로 하강 난류 흐름과, 음의 x 방향 속도 편차는 주로 상향 난류 흐름과 함께 나타난다. 이는 그림 2(f)에서의 결과와 같이 난류에 의한 하향 운동량 플럭스가 우세함을 보여준다. 난류 흐름의 강도는 전반적으로 가열 실험에서 가장 강하고 냉각 실험에서 가장 약하며, 이는 그림 2(d)에서의 결과와 일치한다. 중립 실험과 가열 실험에서 모두 지붕 위 고도에서 연직 방향으로 발달한 난류 고유 구조가 잘 나타나며, 일부는 지붕과 그 아래 고도까지 나타나기도 한다. 반면 냉각 실험에서는 중립 실험 및 가열 실험에서와 달리 지붕 위 고도에서 난류 고유 구조의 크기가 상대적으로 작다. 이러한 결과는 그림 3에서 확인한 바와 같이 중립 실험과 가열 실험에서는 냉각 실험에 비해 상·하층의 난류 고유 구조 간 연관성이 상대적으로 높음을 보여준다. 수평 분포 및 연직 단면에서 나타난 세 실험에서의 난류 고유 구조의 특성 (그림 3과 4)은 다른 시각에서도 유사하게 나타난다. 본 연구에서는 지붕 표면 열 플럭스가 상·하층의 난류 고유 구조 간 연관성에 미치는 영향을 조사하였으나 난류 고유 구조의 발달과 이에 관련된 물리 과정은 상세히 조사되지 않았다. 향후 이와 관련하여 보다 심도있는 분석이 요구된다.

Fig. 4.

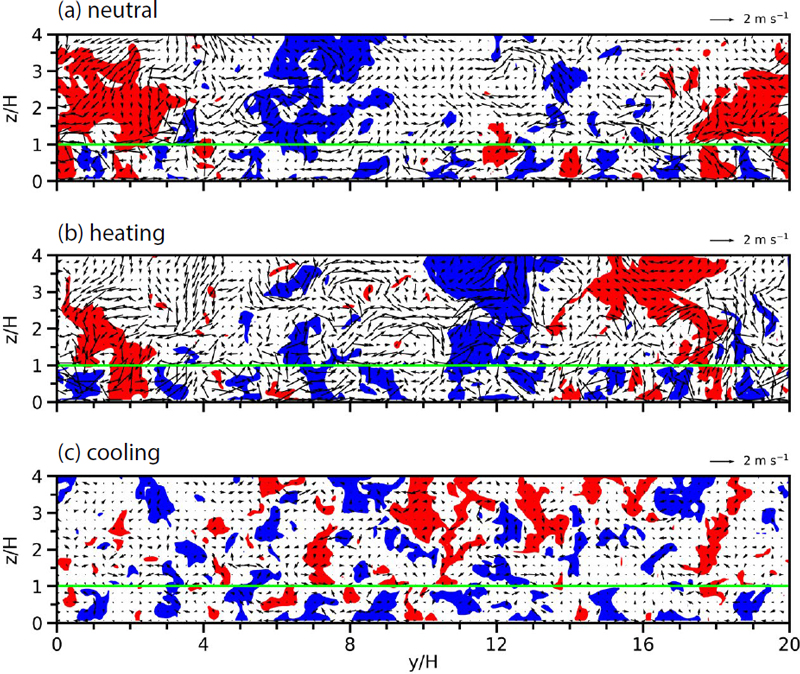
Fields of normalized streamwise velocity deviation and velocity deviation vector at x/H=10 at t=7200 s in the (a) neutral, (b) heating, and (c) cooling simulations. The roof level (z/H=1) is denoted by the green horizontal line. The normalized streamwise velocity deviations larger than 1 and smaller than -1 are indicated by the red and blue shaded areas, respectively.

3. 3 지붕 고도에서의 연직 난류 플럭스

지붕 표면 열 플럭스가 지붕 고도에서의 난류에 의한 운동량, 오염물질, 열 에너지 교환에 미치는 영향을 조사하기 위하여 각 실험에 대해 지붕 고도에서 x 방향 속도 편차 (uʹ)와 연직 속도 편차 (wʹ), 오염물질 농도 편차 (cʹ)와 연직 속도 편차, 온위 편차 (θʹ)와 연직 속도 편차의 결합확률밀도함수에 대한 사분면 분석을 수행하였다 (그림 5). 중립 실험의 경우 θʹ이 0 K이기 때문에 중립 실험에서의 θʹ과 wʹ의 결합확률밀도함수 분포는 제시되지 않았다. 그림 5(a, c, f), 5(b, d, g), 5(e, h)에 나타난 검정색 파선은 각각 |uʹ wʹ|=1 m² s^-2, |cʹ wʹ|=2 μg m^-2 s^-1, |θʹ wʹ|=0.1 K m s^-1 등치선을 의미한다.

Fig. 5.

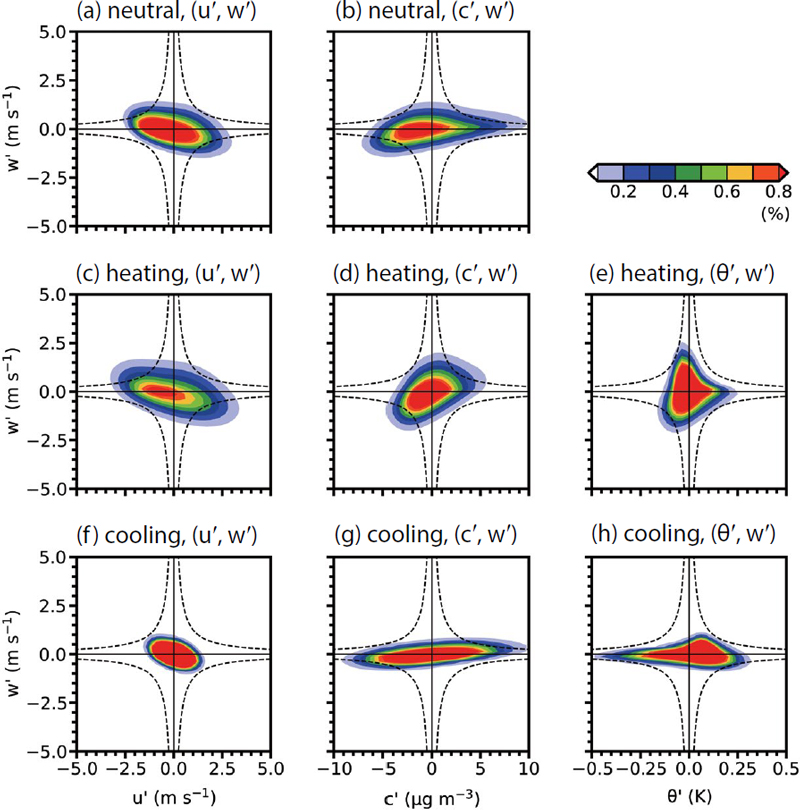
Fields of joint probability density function of (a, c, f ) uʹ and wʹ, (b, d, g) cʹ and wʹ, and (e, h) θʹ and wʹ at z/H=1 in the (a, b) neutral, (c, d, e) heating, and (f, g, h) cooling simulations. The isolines of |uʹwʹ|=1 m2 s-2, |cʹwʹ|=2 μg m-2 s-1, and |θʹwʹ|= 0.1 K m s-1 are indicated by the dashed lines in (a, c, f ), (b, d, g), and (e, h), respectively.

두 임의의 변수쌍 (α, β)에 대하여 결합확률밀도함수는 다음과 같이 계산하였다.

(1)

여기서 a_i와 b_j는 각각 α의 i번째 구간의 중앙값과 β의 j번째 구간의 중앙값을, Δa와 Δb는 각각 α와 β의 구간 너비를 의미한다. 본 연구에서는 uʹ, cʹ, θʹ, wʹ을 너비가 각각 0.25 m s^-1, 0.5 μg m^-3, 0.025 K, 0.25 m s^-1인 40개의 구간으로 나누어 결합확률밀도함수를 계산하였다. uʹ과 wʹ의 결합확률밀도함수의 분포에서는 제1사분면을 외향 상호작용 (outward interaction), 제2사분면을 분출 (ejection), 제3사분면을 내향 상호작용 (inward interaction), 제4사분면을 쓸기 (sweep)로 분류하며, cʹ과 wʹ의 결합확률밀도함수의 분포에서는 제1사분면을 오염물질 분출, 제2사분면을 오염물질 외향 상호작용, 제3사분면을 오염물질 쓸기, 제4사분면을 오염물질 내향 상호작용으로 분류한다 (Kim et al., 2023; Li et al., 2016). θʹ과 wʹ의 결합확률밀도함수의 분포에서는 제1사분면을 온난 상승 (warm updraft), 제2사분면을 한랭 상승 (cold updraft), 제3사분면을 한랭 하강 (cold downdraft), 제4사분면을 온난 하강 (warm downdraft)으로 분류한다 (Chowdhuri et al., 2020).

중립 실험에서는 분출과 쓸기의 빈도가 외향 상호작용과 내향 상호작용의 빈도보다 높으며 (그림 5(a)), 오염물질 분출과 쓸기의 빈도 또한 오염물질 외향 상호작용과 내향 상호작용의 빈도보다 높다 (그림 5(b)). 이는 중립 대기 조건을 고려한 선행 연구의 결과와 일치한다 (Kim et al., 2023). |uʹ wʹ|이 1 m² s^-2을 초과하는 분출과 쓸기의 빈도는 각각 11.5, 16.0%이며, |cʹ wʹ|이 2 μg m^-2 s^-1를 초과하는 오염물질 분출과 쓸기의 빈도는 각각 18.6, 24.0%이다.

가열 실험에서는 uʹ과 wʹ의 결합확률밀도함수의 분포가 중립 실험에서와 유사하게 나타난다 (그림 5(c)). |uʹ wʹ|이 1 m² s^-2을 초과하는 분출과 쓸기의 빈도는 23.0, 25.0%로 중립 실험에서에 비해 더 높다 (그림 5(a)와 5(c)). 이는 가열 실험에서 난류 운동이 더 강하게 나타나는 것과 관련이 있다 (그림 2와 4). 한편 가열 실험에서 cʹ의 분포 범위는 중립 실험에서에 비해 더 좁은 반면, wʹ의 분포 범위는 더 넓다 (그림 5(d)). 가열 실험에서 cʹ의 분포 범위가 더 좁게 나타나는 것은 난류 운동이 더 강하게 나타나 오염물질의 연직 혼합이 강화되어 지붕 고도 근처에서 오염물질 농도의 연직 경도가 감소하는 것과 관련이 있다. |cʹ wʹ|이 2 μg m^-2 s^-1를 초과하는 오염물질 분출과 쓸기의 빈도는 각각 17.8, 20.3%로 중립 실험에 비해 더 낮다. 이는 중립 실험에 비해 가열 실험에서 연직 난류 운동이 더 강하게 나타나 오염물질이 연직적으로 더 잘 확산되어 지붕 고도 근처에서 cʹ의 크기가 감소하였기 때문이다. 가열 실험에서는 한랭 상승과 한랭 하강의 빈도 (35.5, 34.8%)는 온난 상승과 온난 하강의 빈도 (13.4, 16.3%)보다 높다 (그림 5(e)). 도로 표면에서 상향 열 플럭스를 고려한 선행 연구는 온난 상승과 한랭 하강의 빈도가 한랭 상승과 온난 하강의 빈도보다 높게 나타난다 (Efstathiou et al., 2020). 본 연구의 가열 실험에서는 지붕 표면에서 상향 열 플럭스를 고려하였기 때문에 정적으로 불안정한 대기층이 지붕 고도 위에서 나타나며, 지붕 고도 바로 아래에서는 온위가 지붕 고도에서보다 전반적으로 더 낮다. 이로 인해 지붕 고도 아래로부터 상승류에 의한 따뜻한 공기의 수송이 빈 번히 발생하지 않는다. |θʹ wʹ|이 0.1 K m s^-1를 초과 하는 한랭 하강의 빈도는 9.7%인 반면, |θʹ wʹ|이 0.1 K m s^-1를 초과하는 온난 상승은 거의 발생하지 않는다 (0.7%).

냉각 실험에서는 uʹ과 wʹ의 결합확률밀도함수의 분포가 나머지 두 실험에서에 비해 좁게 나타난다 (그림 5(f)). |uʹ wʹ|이 1 m² s^-2을 초과하는 분출과 쓸기의 빈도는 0.6, 0.5%로 매우 낮다. 이는 냉각 실험에서 난류 운동이 약화되는 것과 관련이 있다 (그림 2와 4). 한편 냉각 실험에서 cʹ의 분포 범위는 나머지 두 실험에서에 비해 더 넓은 반면, wʹ의 분포 범위는 더 좁다 (그림 5(g)). 냉각 실험에서 cʹ의 분포 범위가 더 넓게 나타나는 것은 난류 운동이 더 약하게 나타나 오염물질 농도의 연직 경도가 증가하는 것과 관련이 있다. 냉각 실험에서는 온난 상승과 온난 하강의 빈도 (27.7, 26.5%)가 한랭 상승과 한랭 하강의 빈도 (20.2, 24.2%)보다 높다 (그림 5(h)). 한랭 상승의 낮은 빈도는 가열 실험에서와 유사하게 지붕 고도 바로 아래에서의 온위가 지붕 고도에서의 온위보다 전반적으로 더 높은 것과 관련이 있다. |θʹ wʹ|이 0.1 K m s^-1를 초과하는 온난 하강의 빈도는 5.7%인 반면, |θʹ wʹ|이 0.1 K m s^-1를 초과하는 한랭 상승은 거의 발생하지 않는다 (0.3%).

그림 6(a, b, c)는 중립 실험에서 t=7200초일 때 지붕 고도에서의 정규화된 sgn(wʹ)×max(0, -uʹ wʹ), sgn(wʹ)×max(0, cʹwʹ), sgn(wʹ)×max(0, θʹwʹ)의 수평 분포를 보여준다. sgn(wʹ)×max(0,-uʹwʹ), sgn(wʹ)× max(0, cʹwʹ), sgn(wʹ)×max(0, θʹwʹ)은 각각 wʹ의 부호와 하향 난류 운동량 플럭스 크기의 곱, wʹ의 부호와 상향 난류 오염물질 플럭스 크기의 곱, wʹ의 부호와 상향 난류 열 플럭스 크기의 곱을 의미하며, 각각 분출과 쓸기, 오염물질 분출과 쓸기, 온난 상승과 한랭 하강의 강도를 나타낸다. 이들은 각각 난류 운동량 플럭스 표준 편차, 난류 오염물질 플럭스 표준 편차, 난류 열 플럭스 표준 편차로 나누어 정규화하였다. 그림 6(a, b)에서 빨간색으로 나타난 영역은 정규화된 값 이 +1 이상인 영역으로 각각 분출, 오염물질 분출이 강한 영역을 의미하며 파란색으로 나타난 영역은 정규화된 값이 -1 이하인 영역으로 각각 쓸기, 오염물질 쓸기가 강한 영역을 의미한다. 중립 실험에서 강한 분출이 나타나는 영역은 강한 오염물질 분출이 나타나는 영역과 대체로 일치하며, 강한 쓸기가 나타나는 영역은 강한 오염물질 쓸기가 나타나는 영역과 대체로 일치한다 (그림 6(a)와 6(b)). 분석 기간 동안 분출과 오염물질 분출, 쓸기와 오염물질 쓸기 간의 피어슨 상관 계수는 각각 0.63, 0.80으로 강한 상관성을 보이며 통계적으로 유의하다 (p<0.01). 이는 중립 실험에서 비교적 느리고 오염된 공기는 상승하며, 비교적 빠르고 깨끗한 공기는 하강함을 의미한다. 중립 실험의 경우 θʹ이 0 K이기 때문에 온난 상승과 한랭 하강이 나타나지 않는다 (그림 6(c)).

Fig. 6.

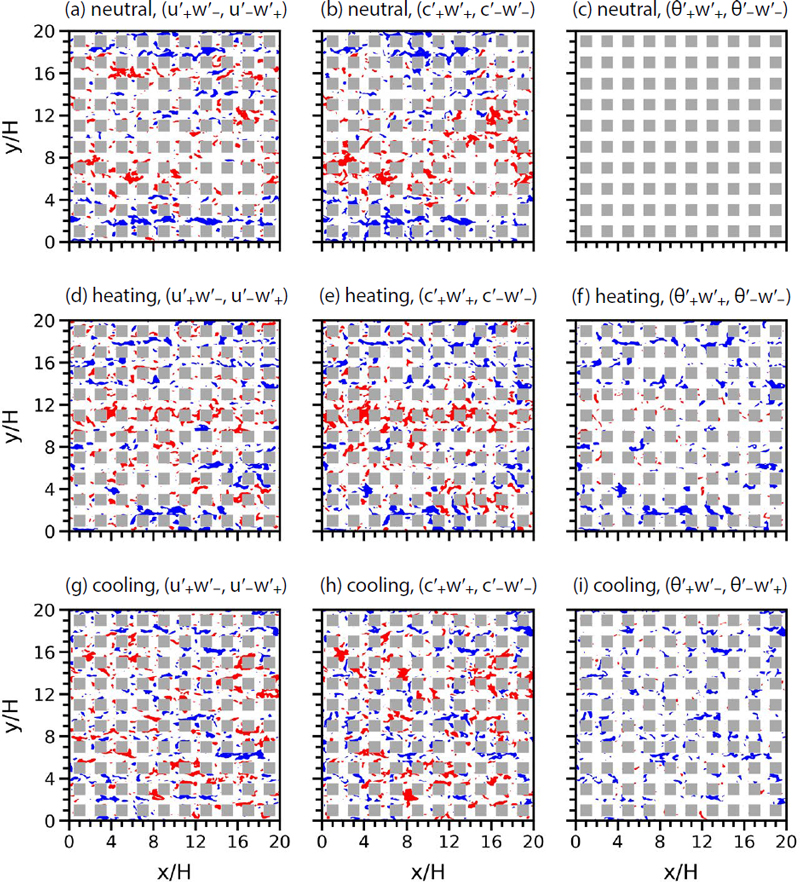
Fields of normalized (a, d, g) sgn(wʹ)×max(0, -uʹwʹ) and (b, e, h) sgn(wʹ)×max(0, cʹwʹ) at z/H=1 at t=7200 s in the (a, b) neutral, (d, e) heating, and (g, h) cooling simulations. Fields of normalized (c, f ) sgn(wʹ)×max(0, θʹwʹ) and (i) sgn(wʹ)×max(0, -θʹwʹ) at z/H=1 at t=7200 s in the (c) neutral, (f ) heating, and (i) cooling simulations. The normalized sgn(wʹ)×max(0, -uʹwʹ), sgn(wʹ)×max(0, cʹwʹ), sgn(wʹ)×max(0, θʹwʹ), and sgn(wʹ)×max(0, -θʹwʹ) larger than 1 and smaller than -1 are indicated by the red and blue shaded areas, respectively.

그림 6(d, e, f)는 가열 실험에서의 수평 분포를 보여준다. 그림 6(f)에서 빨간색, 파란색으로 나타난 영역은 정규화된 값이 각각 +1 이상, -1 이하인 영역으로 각각 온난 상승, 한랭 하강이 강한 영역을 의미한다. 가열 실험에서는 난류에 의한 강한 열 수송 (|θʹ wʹ|> 0.1 K m s^-1)이 한랭 하강에서 가장 뚜렷하게 나타난다 (그림 5(e)). 가열 실험에서도 중립 실험에서와 마찬가지로 강한 분출이 나타나는 영역은 강한 오염물질 분출이 나타나는 영역과 대체로 일치한다. 가열 실험에서 분석 기간 동안 분출과 오염물질 분출 간의 피어슨 상관 계수는 0.65로 통계적으로 유의하다 (p< 0.01). 또한 강한 쓸기가 나타나는 영역은 강한 오염물질 쓸기가 나타나는 영역과 대체로 일치하며 (그림 6(d)와 6(e)) 강한 한랭 하강이 나타나는 영역과도 대체로 일치한다 (그림 6(d)와 6(f)). 분석 기간 동안 쓸기와 오염물질 쓸기, 쓸기와 한랭 하강 간의 피어슨 상관 계수는 각각 0.75, 0.72로 통계적으로 유의하다 (p<0.01). 이는 가열 실험에서 비교적 빠르고 깨끗하며 차가운 공기가 하강함을 의미한다.

그림 6(g, h, i)는 냉각 실험에서의 수평 분포를 보 여준다. 냉각 실험에서는 난류에 의한 강한 열 수송 (|θʹ wʹ|>0.1 K m s^-1)이 온난 하강에서 가장 뚜렷하게 나타난다 (그림 5(h)). 따라서 그림 6(i)에는 그림 6(c, f)와 달리 정규화된 sgn(wʹ)×max(0, -θʹwʹ)가 +1 이상인 영역과 -1 이하인 영역을 나타내었으며, 각각 한랭 상승, 온난 하강이 강한 영역을 의미한다. 나머지 두 실험에서와 마찬가지로, 냉각 실험에서도 강한 분출이 나타나는 영역은 강한 오염물질 분출이 나타나는 영역과 대체로 일치하며 강한 쓸기가 나타나는 영역은 강한 오염물질 쓸기가 나타난다 (그림 6(g)와 6(h)). 냉각 실험에서 분석 기간 동안 분출과 오염물질 분출, 쓸기와 오염물질 쓸기 간의 피어슨 상관 계수는 각각 0.63, 0.72로 통계적으로 유의하다 (p< 0.01). 한편, 강한 쓸기가 나타나는 영역은 강한 온난 하강이 나타나는 영역과 대체로 일치한다 (그림 6(g)와 6(i)). 분석 기간 동안 쓸기와 온난 하강 간의 피어슨 상관 계수는 0.69로 통계적으로 유의하다 (p<0.01). 따라서 가열 실험에서와 달리 냉각 실험에서는 비교적 빠르고 깨끗하며 따뜻한 공기가 하강한다. 그림 6에서 세 실험에 대해 나타난 특성들은 다른 시각에서도 유사하게 나타난다.

3. 4 플러싱과 공동 와류 사건 및 오염물질 분산

강한 분출과 강한 쓸기가 발생할 때 건물 주변에서 나타나는 흐름의 특성과 오염물질 분산을 이해하기 위해 플러싱 (flushing) 사건과 공동 와류 (cavity eddy) 사건을 선별하였다. 플러싱 사건과 공동 와류 사건을 정의하기 위해 두 가지 파라미터 α_f, α_c를 이용하였으며 α_f, α_c는 각각 다음과 같이 정의된다 (Inagaki et al., 2012).

$\[ \begin{array}{c}{\mathrm{\alpha }}_{\mathrm{f}}=\frac{1}{\mathrm{A}}{\int }_0^{\mathrm{H}} {\int }_{0.5\mathrm{H}}^{1.5\mathrm{H}} {\mathrm{I}}_{\mathrm{f}}\left({\mathrm{x}}^{\mathrm{\text{'}}},\mathrm{z}\right){\mathrm{d}\mathrm{x}}^{\mathrm{\text{'}}}dz\\ {\mathrm{I}}_{\mathrm{f}}\left({\mathrm{x}}^{\mathrm{\text{'}}},\mathrm{z}\right)=\left\{\begin{array}{cc}1& \mathrm{ }\mathrm{i}\mathrm{f}\mathrm{ }\mathrm{w}\left({\mathrm{x}}^{\mathrm{\text{'}}},\mathrm{z}\right)>\left|\mathrm{u}\left({\mathrm{x}}^{\mathrm{\text{'}}},\mathrm{z}\right)\right|\\ 0& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\right.\end{array} \]$

(2)

(3)

여기서 xʹ과 yʹ은 그림 7에서 나타난 바와 같이 반복되는 건물 배치에 대해 정의된 좌표계이다. A는 그림 7에서 파란색으로 표시된 지붕 고도 이하 영역의 넓이 (=1024 m²), 겹화살괄호 (<<·>>)는 파란색으로 표시된 영역에서의 평균을 의미한다. αf, αc는 마지막 30분 중 매 1분마다 yʹ/H=1 평면에서만 계산한다. 본 연구에서는 Inagaki et al. (2012)을 따라 α_f 가 0.55 이상인 사건을 플러싱 사건으로, α_c가 0.7 이상인 사건을 공동 와류 사건으로 정의하였다. 플러싱은 건물과 건물 사이에서 상승류가 x 방향 흐름에 비해 우세하게 나타나는 사건이며 (식 (2)), 공동 와류는 건물과 건물 사이에서의 평균적인 흐름에 비해 풍하측 벽면 근처에서 강한 하강류가 나타나는 사건이다 (식 (3)). 플러싱 사건과 공동 와류 사건의 발생률은 중립 실험에서 각각 2.2, 5.6%, 가열 실험에서 각각 2.6, 5.1%, 냉각 실험에서 각각 0.9, 7.2%이다. 중립 실험, 가열 실험, 냉각 실험에서 플러싱 사건의 각각 78.8, 78.4, 69.6%는 지붕 고도에서 분출이 나타나며 공동 와류 사건의 각각 55.5, 56.0, 60.0%는 지붕 고도에서 쓸기가 나타난다. 이는 분출과 쓸기가 각각 플러싱과 공동 와류와 관련이 있음을 보여준다.

Fig. 7.

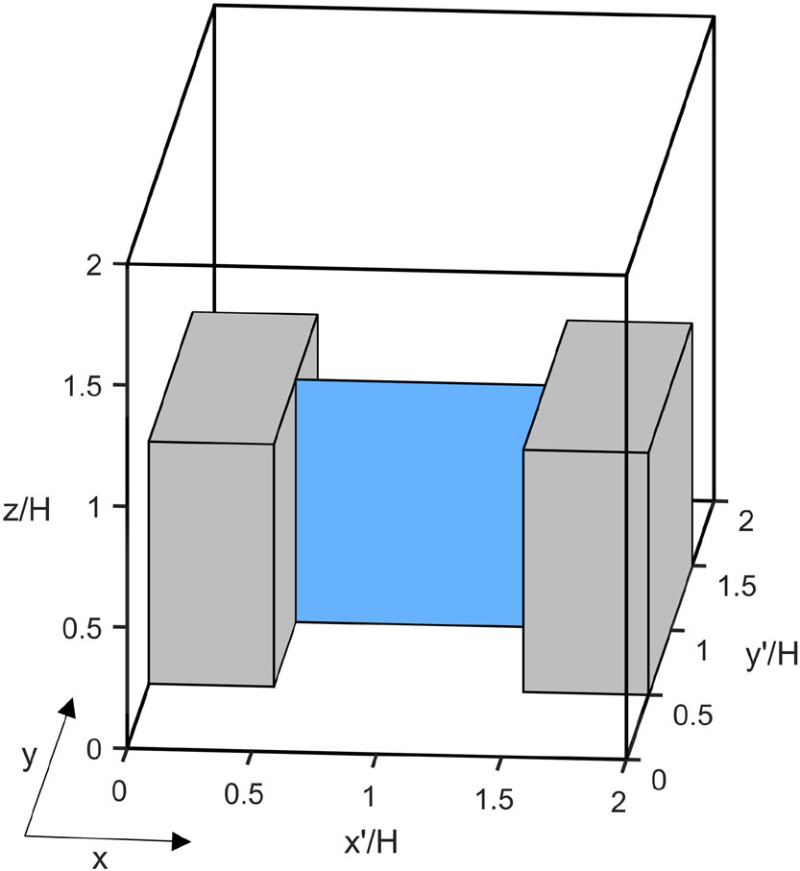
Local coordinates of xʹ and yʹ in each building arrangement. The area at yʹ/H=1 below z/H=1 level is indicated by the blue square.

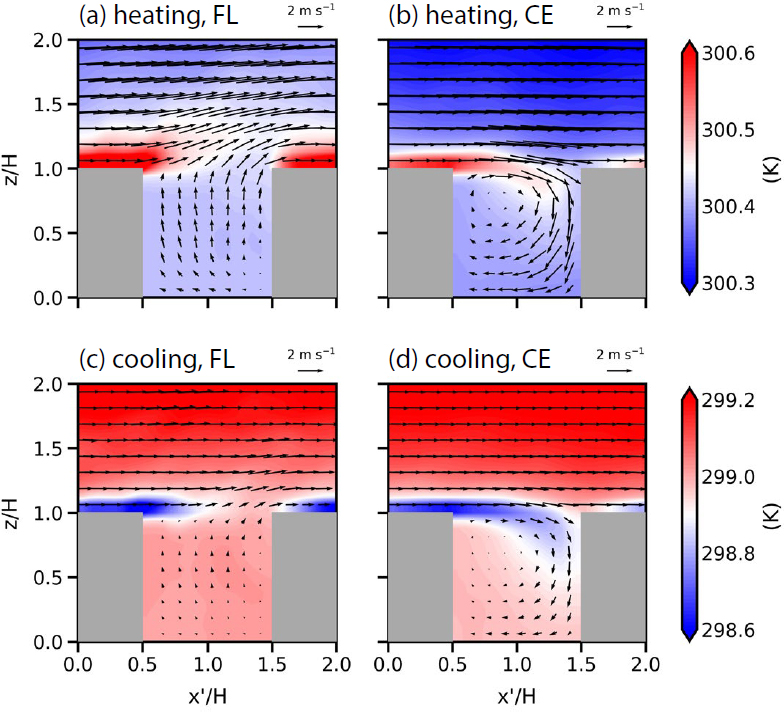
그림 8은 중립 실험, 가열 실험, 냉각 실험에서 각각 플러싱 사건과 공동 와류 사건에 대해 앙상블 평균한 yʹ/H=1에서의 흐름과 오염물질 농도의 연직 단면을 보여준다. 중립 실험에서 플러싱이 발생할 때 yʹ/H=1에서 yʹ 방향 흐름이 수렴하여 상승류가 나타난다 (그림 8(a)). 상승류를 따라 지붕 고도 아래의 오염물질이 지붕 고도 위로 유출된다. 한편 공동 와류가 발생할 때 풍하측 건물 벽면을 따라 강한 하강류가 나타나 지붕 고도 위의 비교적 깨끗한 공기가 지붕 고도 아래로 유입된다 (그림 8(b)). 도로면 근처에서는 yʹ 방향으로 흐름이 발산한다. 플러싱이 발생할 때 건물과 건물 사이에서의 평균적인 상승류의 세기는 가열 실험, 중립 실험, 냉각 실험에서 각각 0.73, 0.47, 0.26 m s^-1로 가열 실험에서 가장 강하게 나타났다. 공동 와류가 발생할 때 풍하측 벽면 근처에서의 평균적인 하강류의 세기는 가열 실험, 중립 실험, 냉각 실험에서 각각 1.79, 1.28, 0.76 m s^-1로 플러싱과 동일하게 가열 실험에서 가장 강하게 나타났다. 따라서 가열 실험에서는 플러싱이 발생할 때 중립 실험 대비 더 강한 상승류에 의해 오염물질이 유출되며, 공동 와류가 발생할 때 중립 실험 대비 더 강한 하강류에 의해 비교적 깨끗한 공기가 유입된다 (그림 8(c)와 8(d)). 냉각 실험에서는 플러싱이 발생할 때 중립 실험 대비 더 약한 상승류에 의해 오염물질이 유출되며, 공동 와류가 발생할 때 또한 중립 실험 대비 더 약한 하강류에 의해 비교적 깨끗한 공기가 유입된다 (그림 8(e)와 8(f)).

Fig. 8.

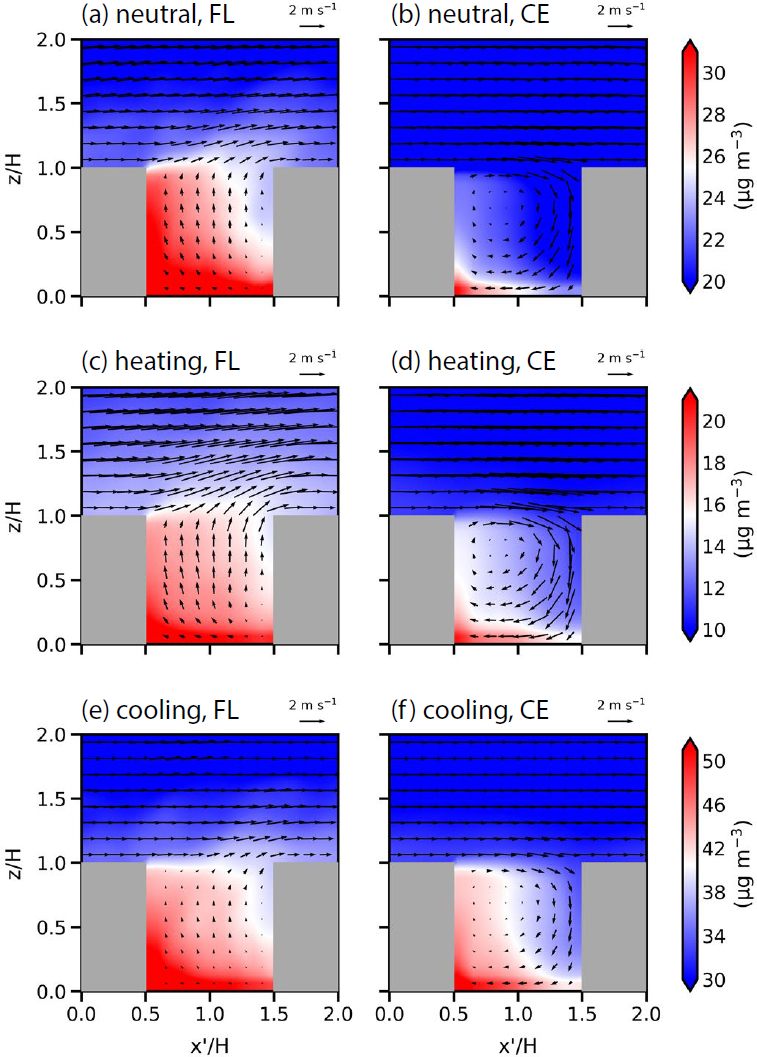
Fields of ensemble-averaged velocity vector and pollutant concentration at yʹ/H=1 for the (a, c, e) flushing (FL) and (b, d, f ) cavity eddy (CE) events in the (a, b) neutral, (c, d) heating, and (e, f) cooling simulations.

그림 9는 가열 실험과 냉각 실험에서 각각 플러싱 사건과 공동 와류 사건에 대해 앙상블 평균한 yʹ/H=1 에서의 흐름과 온위의 연직 단면을 보여준다. 가열 실험에서 플러싱이 발생할 때 상승류에 의해 지붕 근처의 비교적 따뜻한 공기가 상승하며 (그림 9(a)), 공동 와류가 발생할 때 풍하측 지붕 고도 근처에서의 하강류에 의해 지붕 근처의 비교적 따뜻한 공기가 하강한다 (그림 9(b)). 한편 냉각 실험에서 플러싱이 발생할 때는 지붕 근처의 비교적 차가운 공기가 대체로 풍하측 방향으로 이동하는 모습을 보인다 (그림 9(c)). 이는 냉각 실험에서 지붕 고도 위의 대기가 안정하고 플러싱 발생 시 상승류가 약하여 지붕 고도 근처의 비교적 차가운 공기가 연직적으로 이동하지 못하는 것과 관련이 있다. 냉각 실험에서 공동 와류가 발생할 때는 풍하측 지붕 고도 근처에서의 하강류에 의해 지붕 고도 근처의 비교적 차가운 공기가 하강한다 (그림 9(d)).

Fig. 9.

Fields of ensemble-averaged velocity vector and potential temperature at yʹ/H=1 for the (a, c) flushing and (b, d) cavity eddy events in the (a, b) heating and (c, d) cooling simulations.

4. 요약 및 결론

본 연구는 지붕 표면 열 플럭스가 건물 주변의 난류 고유 구조 및 오염물질 분산에 미치는 영향을 조사하였다. 이를 위해 PALM을 이용하여 표면 열 플럭스가 없는 중립 대기 상태를 고려한 경우 (중립 실험), 지붕 표면에서 일정한 상향 열 플럭스를 고려한 경우 (가열 실험), 지붕 표면에서 일정한 하향 열 플럭스를 고려한 경우 (냉각 실험)에 대해 큰 에디 모의를 수행하였다. 가열 실험의 경우 중립 실험에서보다 난류의 세기가 강하고 오염물질 농도가 전반적으로 낮았던 반면, 냉각 실험의 경우 중립 실험에서보다 난류의 세기가 약하고 오염물질 농도가 전반적으로 높았다. 가열 실험과 중립 실험에서는 난류 고유 구조가 수평·연직 방향으로 잘 발달하였고 상·하층에서의 난류 고유 구조 간 유의미한 연관성이 나타났으나, 냉각 실험에서는 난류 고유 구조의 크기가 두 실험에 비해 뚜렷이 작고 지붕 고도 이상에서 상·하층 난류 고유 구조 간 연관성이 거의 나타나지 않았다.

사분면 분석을 수행한 결과 세 실험에서 모두 분출과 쓸기가 가장 빈번하게 나타났으며, 강한 분출이 나타나는 영역은 강한 오염물질 분출이 나타나는 영역과, 강한 쓸기가 나타나는 영역은 강한 오염물질 쓸기가 나타나는 영역과 대체로 일치하였다. 가열 실험에서 한랭 하강의 빈도는 비교적 높았으나 온난 상승의 빈도는 낮았으며, 냉각 실험에서 온난 하강의 빈도는 비교적 높았으나 한랭 상승의 빈도는 낮았다. 지붕 표면 열 플럭스를 고려한 본 연구의 결과는 도로 표면에 상향 (하향) 열 플럭스를 고려할 시 온난 상승 (한랭 상승)이 빈번하게 나타났던 선행 연구의 결과와 차이가 있었다. 쓸기와 분출은 각각 플러싱, 공동 와류와 관련이 있었다. 가열 실험에서는 플러싱, 공동 와류가 발생할 때 중립 실험에서에 비해 더 강한 연직 흐름에 의해 오염물질이 교환되며 강화된 연직 흐름을 따라 지붕 근처의 비교적 따뜻한 공기가 연직 방향으로 이동하였다. 반면 냉각 실험에서는 플러싱, 공동 와류가 발생할 때 중립 실험에서에 비해 더 약한 연직 흐름에 의해 오염물질이 교환된다. 냉각 실험에서 플러싱이 발생할 때 지붕 근처의 비교적 차가운 공기가 대체로 풍하측으로 이동하였으며, 공동 와류가 발생할 때 지붕 근처의 비교적 차가운 공기가 와류를 따라 하강하였다.

본 연구는 건물 지붕면과 인접 대기의 열 교환 특성이 달라질 경우 도시 건물 주변에서의 난류 고유 구조와 오염물질 분산이 어떻게 변화하는지를 탐구하였다. 본 연구의 결과는 기상 조건의 변화 혹은 지붕 특성의 변화로 인한 지붕 표면 열 플럭스의 변화가 도시 흐름과 대기질에 미치는 영향을 보다 잘 이해하는 데에 도움이 될 수 있다. 한편 본 연구에서는 건물 벽 표면과 도로 표면에서의 열 플럭스가 없는 단순한 조건을 고려하였다. 향후 건물 벽면 및 도로 표면의 열 플럭스를 함께 고려하여 표면 열 플럭스의 변화가 흐름과 오염물질 분산에 미치는 영향을 추가적으로 조사하는 것이 필요하다. 실제 도시 지역은 건물 형태 및 배치가 매우 복잡하여 지표면과 인접 대기의 열 교환 특성이 다양하게 나타난다. 실제 도시 지역에 대해 표면 열 플럭스와 흐름 및 오염물질 분산과의 관계를 상세하게 연구하는 것이 필요하다.

본 연구에서 고려된 오염물질은 흐름에 따른 이류 및 확산만이 고려되는 수동적 스칼라 (passive scalar)이다. 수동적 스칼라는 오염물질의 전반적인 이류 및 확산 과정을 조사하는 데에 용이한 반면, 개별 오염물질마다 다른 물리화학적 특성으로 인한 생성 및 제거 과정을 고려하지 못하는 한계가 있다. 예를 들어 오존 및 질소 산화물과 같은 반응성 오염물질의 경우 온도 변화 또는 난류 혼합의 변화가 관련 화학 반응에 영향을 주어 추가적인 농도 변화를 야기할 수 있다 (Qin et al., 2022; Zhang et al., 2020; Bloomer et al., 2009). 향후 다양한 화학 반응을 모의하는 화학 모형과 큰 에디 모의 모형을 결합하여 지표면 열 플럭스가 실제 도시 지역의 오염물질 농도에 미치는 영향에 대해 보다 상세한 연구가 필요하다.

Acknowledgments

본 연구는 한국연구재단의 지원을 받아 수행되었습니다 (2021R1A2C1007044). 본 논문의 개선을 위해 좋은 의견을 제시해주신 두 분의 심사위원께 깊이 감사드립니다.

References

• Akinlabi, E., Maronga, B., Gimetto, M.G., Li, D. (2022) Dispersive fluxes within and over a real urban canopy: a largeeddy simulation study, Boundary-Layer Meteorology, 185, 93-128. [https://doi.org/10.1007/s10546-022-00725-6]
• An, H.-B., Park, S.-B. (2024) Assessing urban ventilation using large-eddy simulations, Building and Environment, 263, 111899. [https://doi.org/10.1016/j.buildenv.2024.111899]
• Belda, M., Resler, J., Geletič, J., Krč, P., Maronga, B., Sühring, M., Kurppa, M., Kanani-Sühring, F., Fuka, V., Eben, K., Benešová, N., Auvinen, M. (2021) Sensitivity analysis of the PALM model system 6.0 in the urban environment, Geoscientific Model Development, 14(7), 4443-4464. [https://doi.org/10.5194/gmd-14-4443-2021]
• Bloomer, B.J., Stehr, J.W., Piety, C.A., Salawitch, R.J., Dickerson, R.R. (2009) Observed relationships of ozone air pollution with temperature and emissions, Geophysical Research Letters, 36(9), L09803. [https://doi.org/10.1029/2009GL037308]
• Boppana, V.B.L., Xie, Z.-T., Castro, I.P. (2014) Thermal stratification effects on flow over a generic urban canopy, Boundary-Layer Meteorology, 153, 141-162. [https://doi.org/10.1007/s10546-014-9935-1]
• Chowdhuri, S., Kumar, S., Banerjee, T. (2020) Revisiting the role of intermittent heat transport towards Reynolds stress anisotropy in convective turbulence, Journal of Fluid Mechanics, 899, A26. [https://doi.org/10.1017/jfm.2020.471]
• Coceal, O., Dobre, A., Thomas, T.G., Belcher, S.E. (2007) Structure of turbulent flow over regular arrays of cubical roughness, Journal of Fluid Mechanics, 589, 375-409. [https://doi.org/10.1017/S002211200700794X]
• Deardorff, J.W. (1980) Stratocumulus-capped mixed layers derived from a three-dimensional model, Boundary-Layer Meteorology, 18, 495-527. [https://doi.org/10.1007/BF00119502]
• Du, Y., Isaxon, C., Roldin, P., Mattisson, K., Karttunen, S., Li, X., Malmqvist, E., Järvi, L. (2024) Large-eddy simulation of aerosol concentrations in a realistic urban environment: model validation and transport mechanism, Environmental Pollution, 358, 124475. [https://doi.org/10.1016/j.envpol.2024.124475]
• Duan, G., Takemi, T., Ngan, K. (2023) Measuring pollutant exposure using large-eddy simulation and virtual walkers: analysis of tracer age statistics of idealised urban boundary-layer flows, Sustainable Cities and Society, 93, 104501. [https://doi.org/10.1016/j.scs.2023.104501]
• Efstathiou, G.A., Thuburn, J., Beare, R.J. (2020) Diagnosing coherent structures in the convective boundary layer by optimizing their vertical turbulent scalar transfer, Boundary-Layer Meteorology, 174, 119-144. [https://doi.org/10.1007/s10546-019-00480-1]
• Fiedler, H.E. (1988) Coherent structures in turbulent flows, Progress in Aerospace Sciences, 25(3), 231-269. [https://doi.org/10.1016/0376-0421(88)90001-2]
• Han, B.-S., Baik, J.-J., Park, S.-B., Kwak, K.-H. (2019) Large-eddy simulations of reactive pollutant dispersion in the convective boundary layer over flat and urban-like surfaces, Boundary-Layer Meteorology, 172, 271-289. [https://doi.org/10.1007/s10546-019-00447-2]
• Inagaki, A., Castillo, M.C.L., Yamashita, Y., Kanda, M., Takimoto, H. (2012) Large-eddy simulation of coherent flow structures within a cubical canopy, Boundary-Layer Meteorology, 142, 207-222. [https://doi.org/10.1007/s10546-011-9671-8]
• Inagaki, A., Kanda, M. (2010) Organized structure of active turbulence over an array of cubes within the logarithmic layer of atmospheric flow, Boundary-Layer Meteorology, 135, 209-228. [https://doi.org/10.1007/s10546-010-9477-0]
• Kanda, M. (2006) Large-eddy simulations on the effects of surface geometry of building arrays on turbulent organized structures, Boundary-Layer Meteorology, 118, 151-168. [https://doi.org/10.1007/s10546-005-5294-2]
• Kanda, M., Moriwaki, R., Kasamatsu, F. (2004) Large-eddy simulation of turbulent organized structures within and above explicitly resolved cube arrays, Boundary-Layer Meteorology, 112, 343-368. [https://doi.org/10.1023/B:BOUN.0000027909.40439.7c]
• Kim, J.-W., Baik, J.-J., Park, S.-B., Han, B.-S. (2023) Impacts of building-height variability on turbulent coherent structures and pollutant dispersion: large-eddy simulations, Atmospheric Pollution Research, 14(5), 101736. [https://doi.org/10.1016/j.apr.2023.101736]
• Lemonsu, A., Grimmond, C.S.B., Masson, V. (2004) Modeling the surface energy balance of the core of an old Mediterranean city: Marseille, Journal of Applied Meteorology and Climatology, 43(2), 312-327. [https://doi.org/10.1175/1520-0450(2004)043%3C0312:MTSEBO%3E2.0.CO;2]
• Li, X.-X., Britter, R., Norford, L.K. (2016) Effect of stable stratification on dispersion within urban street canyons: a large-eddy simulation, Atmospheric Environment, 144, 47-59. [https://doi.org/10.1016/j.atmosenv.2016.08.069]
• Li, X.-X., Britter, R.E., Koh, T.Y., Norford, L.K., Liu, C.-H., Entekhabi, D., Leung, D.Y.C. (2010) Large-eddy simulation of flow and pollutant transport in urban street canyons with ground heating, Boundary-Layer Meteorology, 137, 187-204. [https://doi.org/10.1007/s10546-010-9534-8]
• Lo, K.W., Ngan, K. (2015) Characterising the pollutant ventilation characteristics of street canyons using the tracer age and age spectrum, Atmospheric Environment, 122, 611-621. [https://doi.org/10.1016/j.atmosenv.2015.10.023]
• Maronga, B., Banzhaf, S., Burmeister, C., Esch, T., Forkel, R., Fröhlich, D., Fuka, V., Gehrke, K.F., Geletič, J., Giersch, S., Gronemeier, T., Groß, G., Heldens, W., Hellsten, A., Hoffmann, F., Inagaki, A., Kadasch, E., Kanani-Sühring, F., Ketelsen, K., Khan, B.A., Knigge, C., Knoop, H., Krč, P., Kurppa, M., Maamari, H., Matzarakis, A., Mauder, M., Pallasch, M., Pavlik, D., Pfafferott, J., Resler, J., Rissmann, S., Russo, E., Salim, M., Schrempf, M., Schwenkel, J., Seckmeyer, G., Schubert, S., Sühring, M., von Tils, R., Vollmer, L., Ward, S., Witha, B., Wurps, H., Zeidler, J., Raasch, S. (2020) Overview of the PALM model system 6.0, Geoscientific Model Development, 13(3), 1335-1372. [https://doi.org/10.5194/gmd-13-1335-2020]
• Michioka, T., Sato, A. (2012) Effect of incoming turbulent structure on pollutant removal from two-dimensional street canyon, Boundary-Layer Meteorology, 145, 469-484. [https://doi.org/10.1007/s10546-012-9733-6]
• Michioka, T., Sato, A., Takimoto, H., Kanda, M. (2011) Large-eddy simulation for the mechanism of pollutant removal from a two-dimensional street canyon, Boundary-Layer Meteorology, 138, 195-213. [https://doi.org/10.1007/s10546-010-9556-2]
• Moeng, C.-H., Wyngaard, J.C. (1988) Spectral analysis of largeeddy simulations of the convective boundary layer, Journal of the Atmospheric Sciences, 45(23), 3573-3587. [https://doi.org/10.1175/1520-0469(1988)045%3C3573:SAOLES%3E2.0.CO;2]
• Park, S.-B., Baik, J.-J. (2013) A large-eddy simulation study of thermal effects on turbulence coherent structures in and above a building array, Journal of Applied Meteorology and Climatology, 52(6), 1348-1365. [https://doi.org/10.1175/JAMC-D-12-0162.1]
• Park, S.-B., Baik, J.-J., Han, B.-S. (2015) Large-eddy simulation of turbulent flow in a densely built-up urban area, Environmental Fluid Mechanics, 15, 235-250. [https://doi.org/10.1007/s10652-013-9306-3]
• Qin, Z., He, Y., Zhao, X., Feng, Y., Yi, X. (2022) A case analysis of turbulence characteristics and ozone perturbations over eastern China, Frontiers in Environmental Science, 10, 970935. [https://doi.org/10.3389/fenvs.2022.970935]
• Resler, J., Eben, K., Geletič, J., Krč, P., Rosecký, M., Sühring, M., Belda, M., Fuka, V., Halenka, T., Huszár, P., Karlický, J., Benešová, N., Ďoubalová, J., Honzáková, K., Keder, J., Nápravníková, Š., Vlček, O. (2021) Validation of the PALM model system 6.0 in a real urban environment: a case study in Dejvice, Prague, the Czech Republic, Geoscientific Model Development, 14(8), 4797-4842. [https://doi.org/10.5194/gmd-14-4797-2021]
• Roth, M. (2000) Review of atmospheric turbulence over cities, Quarterly Journal of the Royal Meteorological Society, 126(564), 941-990. [https://doi.org/10.1002/qj.49712656409]
• Saiki, E.M., Moeng, C.-H., Sullivan, P.P. (2000) Large-eddy simulation of the stably stratified planetary boundary layer, Boundary-Layer Meteorology, 95, 1-30. [https://doi.org/10.1023/A:1002428223156]
• Takimoto, H., Inagaki, A., Kanda, M., Sato, A., Michioka, T. (2013) Length-scale similarity of turbulent organized structures over surfaces with different roughness types, Boundary-Layer Meteorology, 147, 217-236. [https://doi.org/10.1007/s10546-012-9790-x]
• Tian, G., Ma, Y., Chen, Y., Wan, M., Chen, S. (2024) Impact of urban canopy characteristics on turbulence dynamics: insights from large eddy simulation, Building and Environment, 250, 111183. [https://doi.org/10.1016/j.buildenv.2024.111183]
• Trimmel, H., Weihs, P., Faroux, S., Formayer, H., Hamer, P., Hasel, K., Laimighofer, J., Leidinger, D., Masson, V., Nadeem, I., Oswald, S.M., Revesz, M., Schoetter, R. (2019) Thermal conditions during heat waves of a mid-European metropolis under consideration of climate change, urban development scenarios and resilience measures for the mid-21st century, Meteorologische Zeitschrift, 30(1), 9-32. [https://doi.org/10.1127/metz/2019/0966]
• Yazid, A.W.M., Sidik, N.A.C., Salim, S.M., Saqr, K.M. (2014) A review on the flow structure and pollutant dispersion in urban street canyons for urban planning strategies, Simulation, 90(8), 892-916. [https://doi.org/10.1177/0037549714528046]
• Yoshida, T., Takemi, T. (2021) Spatial characteristics of turbulent organized structures within the roughness sublayer over idealized urban surface with obstacle-height variability, Environmental Fluid Mechanics, 21, 129-154. [https://doi.org/10.1007/s10652-020-09764-4]
• Zhang, Y., Ou, C., Chen, L., Wu, L., Liu, J., Wang, X., Lin, H., Gao, P., Hang, J. (2020) Numerical studies of passive and reactive pollutant dispersion in high-density urban models with various building densities and height variations, Building and Environment, 177, 106916. [https://doi.org/10.1016/j.buildenv.2020.106916]