Super Learner 앙상블을 활용한 PM_2.5 예측

1. 서 론

미세먼지는 대기 오염 물질 중 하나로, 입자의 크기에 따라 직경이 10 μm 이하인 PM₁₀와 2.5 μm 이하인 PM_2.5로 구분된다. 이는 사람의 머리카락 직경 (약 60 μm)보다 작아 눈에 보이지 않지만 사회 및 인체에 부정적인 영향을 주고 있다. 특히, 입자가 미세한 PM_2.5는 혈관, 폐포 등 인체의 깊숙한 곳까지 침투할 수 있어 인체에 큰 영향을 미칠 수 있다. Bae (2014)에 의하면 미세먼지 농도의 증가는 심혈관계 초과사망발생위험을 높이며 PM₁₀보다 PM_2.5에 의한 초과사망 발생위험이 다소 높은 것으로 나타났다. 이에 따라 정부는 고농도 PM_2.5가 일정 기간 지속될 경우, 대기질을 개선하기 위해 대기 배출 사업장 및 공사장의 가동시간을 조절하거나 차량의 운행을 제한하는 미세먼지 비상저감조치를 시행하고 있다. 비상저감조치는 당일 평균 PM_2.5 관측 농도와 다음날 예보 농도가 50 μg/m³ 초과인 경우, 당일 주의보 또는 경보가 발령되고 다음날 예보 농도가 50 μg/m³ 초과인 경우, 다음날 예보 농도가 75 μg/m³ 초과인 경우 중 하나라도 해당하면 발령된다. 즉, 비상저감조치는 다음날 예측치를 기준으로 발령되기 때문에 사업장의 불필요한 제한이나 고농도 PM_2.5로 인한 피해를 막기 위해서는 PM_2.5 농도의 정확한 예측이 중요하다. 뿐만 아니라, PM_2.5 농도의 정확한 예측은 야외활동 계획이나 건강을 보호하는 등 PM_2.5로부터 발생하는 피해를 사전에 예방할 수 있도록 국민들에게 정보를 제공할 수 있다.

미세먼지는 발생원에 따라 1차, 2차 미세먼지로 나뉘는데 소각이나 배기가스로 인한 미세먼지 혹은 도로나 공장 등에서 발생하는 먼지가 1차 미세먼지에 속한다. 반면, 2차 미세먼지는 1차 발생원에서 배출된 대기 오염 물질이 대기 중 떠다니는 전구물질과 화학반응을 일으켜 생성되며, 이러한 화학반응에 의해 생성된 2차 생성 미세먼지의 비중이 PM_2.5의 약 2/3를 차지할 만큼 매우 높은 것으로 알려져 있다 (ME, 2016). 미세먼지 생성에 영향을 주는 대기 오염 물질은 관측 자료의 수집이 비교적 쉽고 최근 기계학습 기법이 발전함에 따라 과거 관측 자료를 활용한 기계학습 기반의 미세먼지 등급 또는 농도 예측 연구가 이루어지고 있다 (Kim and Jeong, 2022; Kim and Moon, 2021; Park, 2021).

기계학습 기법의 하나인 앙상블 기법은 여러 모형의 예측을 결합함으로써 보다 나은 예측을 갖도록 하는 방법으로, 여러 모형의 예측을 평균하거나 투표를 통해 최종 예측하며 회귀와 분류 문제에 모두 적용될 수 있다. 또한, 여러 모델의 예측을 결합하기 때문에 예측의 변동을 줄여 모델의 안정성을 높이고 단일 모델에 비해 정확한 예측이 가능하다. 그러나, 입력되는 모델의 다양성으로 인해 결과의 해석이 어렵고, 각 모델의 기여도와 중요성을 파악하기 어려운 측면이 있기 때문에 목적에 맞게 앙상블 모델을 선택하는 것이 중요하다. 앙상블 기법은 크게 Bagging, Boosting, Stacking으로 나뉜다. Bagging (Breiman, 1996)은 여러 개의 부트스트랩 자료를 통해 학습된 여러 단일 모델의 예측을 결합하여 분산을 낮추는 기법으로, Random Forest가 대표적이다. Lee and Lee (2020)는 시간당 PM_2.5 농도를 예측하기 위해 대기 및 기상 관측 시계열 데이터를 전처리하여 Random Forest를 학습한 결과, 시계열 학습에서 강점을 갖는 LSTM 보다도 성능이 우수했으며 예측 결과에 대해 설명 가능한 모델임을 보여주었다. Boosting은 예측력이 약한 모형을 순차적으로 결합하여 강한 모형을 만드는 기법이다. 부트스트랩 샘플을 단일 모델이 독립적으로 학습하는 bagging과 달리, boosting은 이전 모델의 예측 결과를 반영하여 학습 샘플에 가중치를 부여하면서 순차적으로 학습한다. Boosting은 학습 속도가 느리고 노이즈에 민감하지만, 대체로 단일 모델보다 향상된 예측 성능을 갖는다. Park et al. (2021)은 PM₁₀ 및 PM_2.5 농도를 추정하기 위해 Boosting 기반의 대표적인 기법인 Gradient Boosting과 LightGBM을 적용하고 비교 분석하였으며, Kim (2020)은 PM_2.5 등급을 분류하기 위해 eXtreme Gradient Boosting (XGBoost)을 앙상블하여 단일 XGBoost보다 향상된 예측 결과를 보여주었다. Stacking (Wolpert, 1992)은 다양한 종류의 단일 모델의 예측을 결합하는 기법으로, 병렬로 학습한 단일 모델의 예측 값을 메타 모델의 입력 데이터로 학습하여 최종 예측한다. 서로 다른 유형의 모델을 결합하기 때문에 데이터의 다양한 패턴을 학습할 수 있으며 단일 모델과 메타 모델의 다양성으로 인해 확장 가능하다는 특징이 있다. Danesh Yazdi et al. (2020)은 런던 지역의 PM_2.5 농도 예측을 위해 Random Forest, Gradient Boosting Machine, K-nearest neighbor의 예측 결과를 generalized additive model로 결합하였다. Zhai and Chen (2018)은 Lasso, Adaboost, XGBoost, GA-MLP의 예측 결과를 Support Vector Machine으로 결합하여 베이징의 일평균 PM_2.5 농도를 예측한 바 있다.

본 연구는 대기 오염 물질 관측 자료를 활용하여 서울시 중구의 시간당 PM_2.5 농도를 예측하기 위해 Stacking 기법을 적용하고 단일 모델과 예측 성능을 비교 분석하고자 한다. Stacking 기법을 기반으로 PM_2.5 농도를 예측한 선행 연구에 비해 보다 다양한 7가지 단일 모델을 적용하였으며, 이들의 예측을 가중 결합하는 Super Learner를 통해 최종 예측하였다. 2장에는 예측에 사용된 자료와 여러 기계학습 방법들에 대한 간략한 설명 및 이들을 결합한 Super Learner를 설명한다. 3장에서는 방법 간 예측 결과 및 성능을 평가하고 마지막 장에는 결론 및 향후 연구 방향을 제시한다.

2. 자료 및 방법

2. 1 관측 자료

국립환경과학원의 대기환경연보 (NIER, 2022)에 따르면, PM_2.5는 상당량이 황산화물 (SO_x), 질소산화물 (NO_x), 암모니아 (NH₃), 휘발성 유기화합물 (VOCs) 등의 전구 물질이 대기 중의 특정 조건에서 반응하여 2차 생성되는 것으로 알려져 있다. 이에 따라 본 연구에서는 대기 오염 물질과 PM_2.5 간의 관계를 파악하고 이를 설명 변수로 활용하여 PM_2.5 농도를 예측하고자 한다. 분석에 사용된 자료는 에어코리아로부터 수집된 대기 오염 물질의 최종 확정 자료이다. 관측 지점은 서울시 중구 도시 대기 측정소로, 해당 측정소에서 관측된 SO₂, CO, O₃, NO₂, PM₁₀, PM_2.5의 시간당 자료를 수집하였다. 수집 기간은 2018년 12월 1일 1시부터 2021년 11월 30일 24시까지 총 3년간의 자료이다. 시간당 자료 중 모든 변수가 누락되지 않은 자료만 구축하여 총 24,414개의 자료를 수집하였다. 특히, 2019년 7월 26일 1시~9월 18일 17시에 관측된 CO 데이터가 누락되어 해당 기간의 시간 자료는 사용하지 않았다. 연구에 사용된 훈련 및 검증 집합에 대한 정보는 표 1에 주어져 있다. 수집된 전체 기간 중 2년 (2018년 12월 1일 1시~2020년 11월 30일 24시)을 훈련 집합으로 사용하고, 이후의 1년 (2020년 12월 1일 1시~2021년 11월 30일 24시)을 검증 집합으로 사용하여 검증 집합에 대한 여러 기계학습 기법 간 예측 결과를 비교하고자 한다.

Table 1.

Description of the dataset.

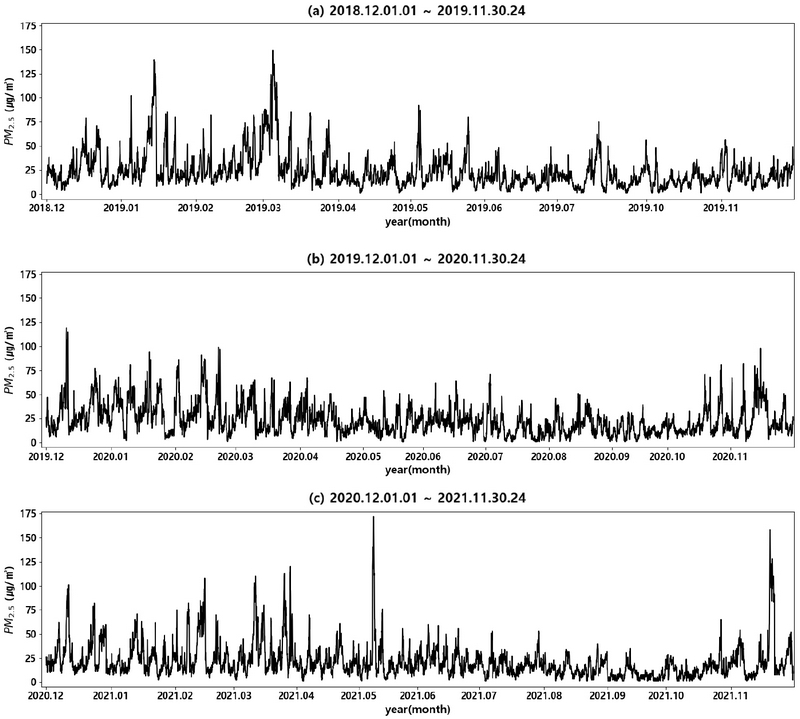
그림 1의 (a), (b), (c)는 각각 1년간의 PM_2.5 농도 추이를 나타낸 그래프이다. 모든 연도에서 여름철과 가을철에 PM_2.5 농도가 비교적 낮으며 겨울철과 봄철에 높게 나타났다. 훈련 기간에 속하는 2018년 12월~2020년 11월 (그림 1(a), (b))에는 최대 150 μg/m³의 고농도 PM_2.5가 관측되었지만 검증 기간에 속하는 그림 1(c)의 경우 황사 및 대기 정체의 영향으로 2021년 5월에 172 μg/m³, 2021년 11월에 158 μg/m³의 고농도 PM_2.5가 관측되었음을 볼 수 있다.

Fig. 1.

Time series data of PM2.5 according to each year.

표 2는 PM_2.5를 예측하기에 앞서 수집된 자료에 대한 탐색적 데이터 분석의 결과로, 각 변수들의 기술 통계량을 나타낸다. 모든 변수는 0 또는 양의 값을 갖는 양적 자료로, 설명 변수 중 SO₂, CO, O₃, NO₂는 최대 2 ppm으로 매우 작은 값을 갖는 반면, PM₁₀과 PM_2.5는 각각 최대 1024 μg/m³, 172 μg/m³의 값을 갖는다. 일부 회귀모형에서는 상대적으로 넓은 범위의 값을 갖는 PM₁₀의 영향력이 크게 작용할 수 있어 최소-최대 정규화를 적용하여 모든 변수가 0부터 1사이의 값을 갖도록 하였다. 또한, 수집된 대기 관측 자료들은 최종 확정 자료의 유효자리수에 따라 SO₂, O₃, NO₂는 소수점 넷째 자리, CO는 소수점 둘째 자리, PM₁₀ 및 PM_2.5는 소수점 첫째 자리에서 반올림하였다. 이에 따라 PM_2.5 농도 예측 값도 소수점 첫째 자리에서 반올림한 양의 정수 값을 사용하였다.

Table 2.

Descriptive statistics of the explanatory and dependent variables.

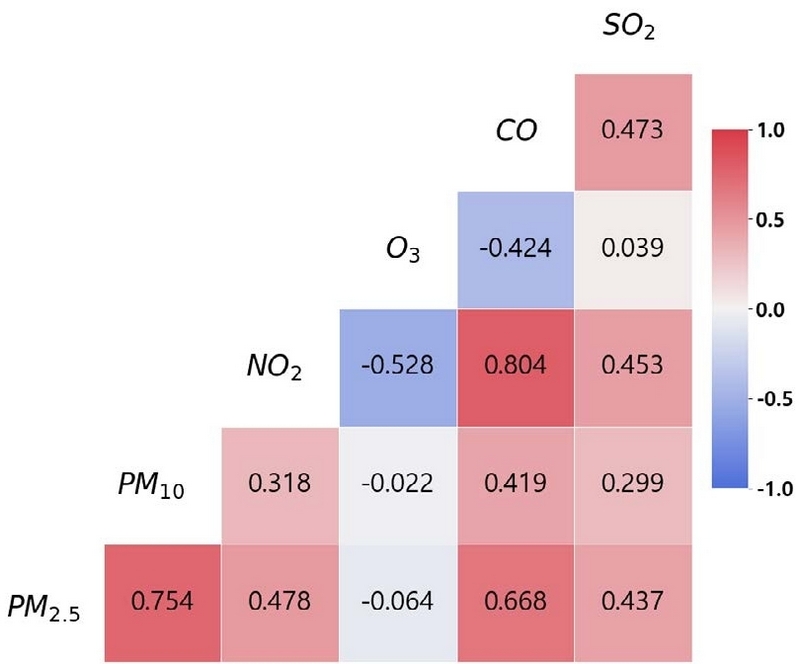
변수 간의 선형적 관계를 확인하기 위한 상관계수 행렬이 그림 2에 주어져 있다. 예측 대상인 PM_2.5는 PM₁₀ 및 CO와 각각 0.7, 0.6 이상의 강한 양의 상관관계를 보이고 있으며, NO₂ 및 SO₂와 0.4 이상의 약한 양의 상관관계를 갖는다. 반면, O₃는 -0.064로 PM_2.5와 상관관계가 없다고 해석할 수 있지만 다른 대기 오염 물질과의 반응을 통해 PM_2.5 농도에 영향을 미칠 수 있을 것으로 판단하여 설명 변수로 사용하였다.

Fig. 2.

Correlations between PM2.5 and the explanatory variables.

2. 2 연구 방법

본 연구에서는 대기 오염 물질과 PM_2.5 사이의 관계를 기반으로 시간당 PM_2.5 농도를 예측하기 위해 Super Learner 앙상블을 적용하였다. Van der Laan et al. (2007)에 의해 제안된 Super Learner는 다양한 기계학습 알고리즘을 가중 결합하는 앙상블 기법이다. Super Learner 알고리즘에 대한 자세한 설명은 표 3에 주어져 있다 (Polley and Van der Laan, 2010). 표 3에 주어진 알고리즘의 기본 개념은 기저 학습기 (base learner)라고 불리는 여러 기계학습 알고리즘의 결과를 결합할 때 cross-validation을 기반으로 오차를 최소화하는 최적의 기저 학습기 조합을 찾는 것이다. cross-validation은 학습 데이터를 동일한 크기의 폴드로 나눈 후 하나를 검증 데이터로, 나머지를 훈련 데이터로 사용하는 과정을 반복하여 학습함으로써 학습 데이터에 과적합되는 것을 방지하거나 모델의 일반화 성능을 평가하는 데 사용된다. Super Learner는 cross-validation을 통해 누적된 기저 학습기들의 예측 값을 기반으로 최적의 알고리즘 조합을 찾음으로써 모델의 일반화 성능을 향상시킨다. 또한, 양수이고 합이 1이 되도록 제한된 기저 학습기의 가중치를 추정함으로써, 이들의 가중치를 통해 기저 학습기의 기여도를 해석할 수 있다. 본 연구에서는 7개의 기계학습 알고리즘으로 선형회귀, Support Vector Machine, K-Nearest Neighbors, Decision Tree, Random Forest, Gradient Boosting, eXterme Gradient Boosting을 기저 학습기로 갖는 Super Learner를 적용하였으며, PM_2.5의 Super Learner 앙상블 예측치들은 표 3에 주어진 학습 알고리즘의 방법을 통해 추정하였다.

Table 3.

Learning process of the Super learning algorithm.

기저 학습기로 사용된 선형회귀 (Linear Regression)는 종속 변수와 한 개 이상의 독립 변수와의 선형 상관관계를 모델링하여 독립 변수들이 종속 변수에 미치는 영향과 종속 변수의 값을 추정한다. 회귀 계수는 실제 값과 모델에서 얻어지는 추정 값 사이의 오차를 최소화하는 최소자승법 (Ordinary Least Square, OLS) 또는 오차항에 대한 가정을 기반으로 우도를 최대화하는 최대우도법 (Maximum Likelihood Estimation, MLE)을 통해 추정된다. Support Vector Machine은 결정 경계를 통해 데이터를 분리하는 방법으로, 결정 경계 중 데이터들과 가장 거리가 먼 결정 경계를 찾아 데이터를 분류하거나 예측한다. 또한, 선형적으로 분리하기 어려운 비선형 데이터는 커널 함수를 통해 고차원 공간으로 매핑하여 초평면을 찾을 수 있다. 거리 기반 알고리즘인 K-Nearest Neighbors는 새로운 데이터가 주어졌을 때, 기존 데이터 가운데 가장 가까운 k개의 이웃 데이터를 기반으로 예측 및 분류를 수행한다. 단순하고 직관적이지만 데이터의 크기에 따라 계산 비용이 증가하며, k값에 따라 모델의 성능이 달라지므로 적절한 k를 선택하는 것이 중요하다. 트리 형태의 알고리즘인 Decision Tree는 분석 과정이 직관적이고 이해하기 쉬운 특징이 있다. 분할의 기준이 되는 변수와 임계값은 분류 문제에서는 지니 지수 또는 엔트로피 지수를 기반으로 불순도가 작아지도록 기준이 결정되며, 회귀 문제에서는 분산 감소량을 최대화하거나 평균 제곱 오차가 작아지는 방향으로 결정된다. 그러나 트리의 깊이가 깊을수록 과적합 위험이 있기 때문에 사전에 트리의 깊이를 제한하거나 불필요한 가지를 제거하는 추가 작업이 필요하다. Random Forest는 Bagging의 대표적인 알고리즘으로, 여러 개의 Decision Tree를 결합함으로써 과적합 위험이 높은 Decision Tree를 보완한다. 이는 부트스트랩 샘플을 통해 트리들의 편향은 유지하면서, 개별 트리의 분리 기준에 사용되는 변수의 후보를 랜덤하게 선택하여 트리 간의 상관성을 낮추어 일반화 오류를 줄일 수 있다 (Breiman, 2001). Gradient Boosting은 약한 분류기를 결합하여 강한 분류기를 생성하는 Boosting 기법의 한 종류로, 일반적으로 약한 분류기로 트리가 사용된다. 이전 트리가 남긴 오차를 경사 하강법을 기반으로 손실 함수를 최소화하도록 다음 트리가 학습된다. 오차를 계속해서 줄여나가는 방식으로 학습되기 때문에 정확도가 높으나 노이즈가 있을 경우 과적합이 발생할 수 있으며, 훈련 시간이 오래 걸리는 단점이 있다. Gradient Boosting의 단점을 보완하는 eXtreme Gradient Boosting (Chen and Guestrin, 2016)은 예측 성능이 우수해 분류 및 회귀 문제의 여러 영역에서 사용되는 기계학습 기법 중 하나이다. 약한 분류기인 트리를 생성하는 과정에서 데이터를 일정 간격으로 나누고 그 안에서 최적의 분기점을 찾음으로써 병렬 처리가 가능해 학습 속도를 높일 수 있다. 또한, 이전 트리가 남긴 오차를 학습하는 과정에서 손실 함수에 패널티를 부과해 가중치를 규제함으로써 과적합을 방지할 수 있다.

3. 결 과

본 절에서는 앞서 설명한 기계학습 모델을 적용하고 검증 기간에 대한 예측 성능을 비교하고자 한다. 먼저, 기저 학습기의 최적의 하이퍼 파라미터를 추정하기 위해 GridSearchCV를 적용하였다. GridSearchCV는 cross-validation을 적용해 주어진 하이퍼파라미터의 조합을 고려하여 모델의 성능을 기반으로 최적의 하이퍼파라미터를 찾는 방법이다. 이는 데이터 수와 변수 조합이 많을 경우 많은 시간이 소요되기 때문에 본 연구에서는 표 4에 주어진 것과 같이 기계학습 모델당 최대 2가지 하이퍼파라미터를 고려하여 최적의 값을 찾아 모델을 최적화하였다. 또한, 선형회귀와 Support Vector Machine은 모델의 특성상 음의 예측 값이 발생할 수 있다. 이러한 경우 예측 값을 0으로 처리하였다.

Table 4.

Hyper-parameter information for the base learners.

최적화된 모델을 기반으로 Super Learner를 학습하였을 때 추정된 기저 학습기의 가중치는 표 5과 같다. 이는 0의 가중치를 갖는 Support Vector Machine (SVM), K-Nearest Neighbors (KNN), Gradient Boosting (GBM)은 Super Learner의 예측에 전혀 영향을 주지 않았으며, Random Forest (RF) (0.38169), eXtereme Gradient Boosting (XGB) (0.30246), 선형회귀 (LR) (0.29331) 순으로 크게 기여를 하였음을 의미한다.

Table 5.

Estimated weights of the base learners, which include LR (Linear Regression), SVM (Support Vector Machine), KNN (K-Nearest Neighbors), DT (Decision Tree), RF (Random Forest), GBM (Gradient Boosting), and XGB (eXtreme Gradient Boosting).

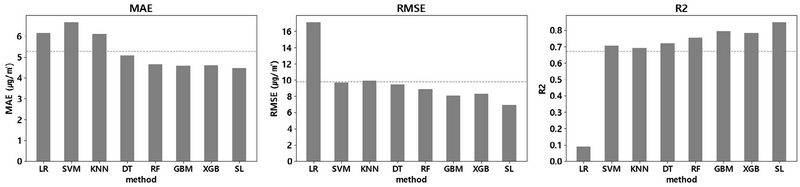
검증 기간에 대한 예측 성능이 그림 3 및 표 6에 주어져 있으며 그림 3의 점선은 모든 모델들의 평균 성능을 보여준다. 각 성능 지표의 평균값은 MAE가 5.2905 μg/m³, RMSE가 9.8015 μg/m³, R²가 0.6739로 나타났다. 기저 학습기 중 선형회귀 (LR)의 MAE는 6.1703 μg/m³, Support Vector Machine (SVM)의 MAE는 6.6662 μg/m³, K-Nearest Neighbors (KNN)의 MAE는 6.1119 μg/m³로, 평균 MAE (5.2905 μg/m³)에 비해 예측 오차가 다소 크게 나타났다. 특히, 선형회귀 (LR)는 모든 모델 중 RMSE가 17.095 μg/m³로 가장 크고, R²는 0.0881로 가장 작으며 이는 예측 농도가 관측 농도를 제대로 설명하지 못하고 있음을 의미한다. Decision Tree (DT)는 MAE가 5.0715 μg/m³, RMSE가 9.4741 μg/m³, R²가 0.7199로 평균보다 약간 개선된 예측 성능을 갖는다. 반면, 앙상블 기법인 Random Forest (RF), Gradient Boosting (GBM), eXtreme Gradient Boosting (XGB)은 모든 성능 지표에서 평균 이상의 예측 성능을 보이고 있다. 이를 통해 앙상블 기법이 다른 기저 학습기보다 예측이 정확하게 이루어졌음을 알 수 있다. 특히, Super Learner (SL)의 MAE가 4.4653 μg/m³, RMSE가 6.9530 μg/m³로 적용된 모든 모델 중 예측 오차가 가장 작으며 R²는 0.8491로 결정 계수가 가장 큰 것으로 나타났다. 즉, Super Learner는 모든 성능 지표에서 예측 성능이 가장 우수했으며 평균 이상의 성능을 갖는 다른 앙상블 기법에 비해서도 개선된 결과를 보여주고 있다.

Fig. 3.

Comparisons of MAE, RMSE and R2 for the base learners and Super Learner.

Table 6.

Prediction performances of the base learners from the seven machine learning algorithms and the Super Learner in terms of MAE, RMSE and R2.

검증 기간에 대하여 관측된 PM_2.5 농도와 각 방법의 예측 농도를 비교한 그래프가 그림 4에 주어져 있다. x축과 y축은 각각 관측 농도와 예측 농도를 나타내며 관측 농도와 예측 농도가 일치할수록 관측 농도와 예측 농도들이 45도 직선에 가깝게 위치하게 되고 이것은 예측이 정확하게 이루어졌다고 해석할 수 있다. 선형회귀 (LR)와 Support Vector Machine (SVM) (그림 4(a), (b))은 관측 농도에 비해 크게 예측하는 결과를 보였으며, 특히 선형회귀 (LR)는 고농도 관측치를 최대 500 μg/m³ 이상의 매우 큰 값으로 예측하였다. 한편, K-Nearest Neighbors (KNN) (그림 4(c))은 다른 기저 학습기에 비해 작게 예측하는 경향을 보이고 있다. Decision Tree (DT) (그림 4(d))의 경우 훈련된 트리의 터미널 노드에 따라 예측 값이 생성되기 때문에 예측 값이 다양하지 않으며, 저농도 관측치는 크게 예측하고 고농도 관측치는 작게 예측하는 결과를 보였다. 그 외 앙상블 기법인 Random Forest (RF), Gradient Boosting (GBM), eXtreme Gradient Boosting (XGB) (그림 4(e), (f), (g))은 서로 비슷한 예측 분포를 띠고 있으며, 이들은 공통적으로 고농도 관측치에 대한 정확도가 떨어지는 모습을 보이고 있다. 반면, 기저 학습기들의 예측을 가중 결합한 Super Learner (SL) (그림 4(h))는 다소 크게 예측하는 경우가 존재하지만 대체로 45도 직선 주위에 분포하며 기저 학습기들이 정확하게 예측하지 못한 고농도 관측치에 대해서 가장 정확하게 예측하고 있다.

Fig. 4.

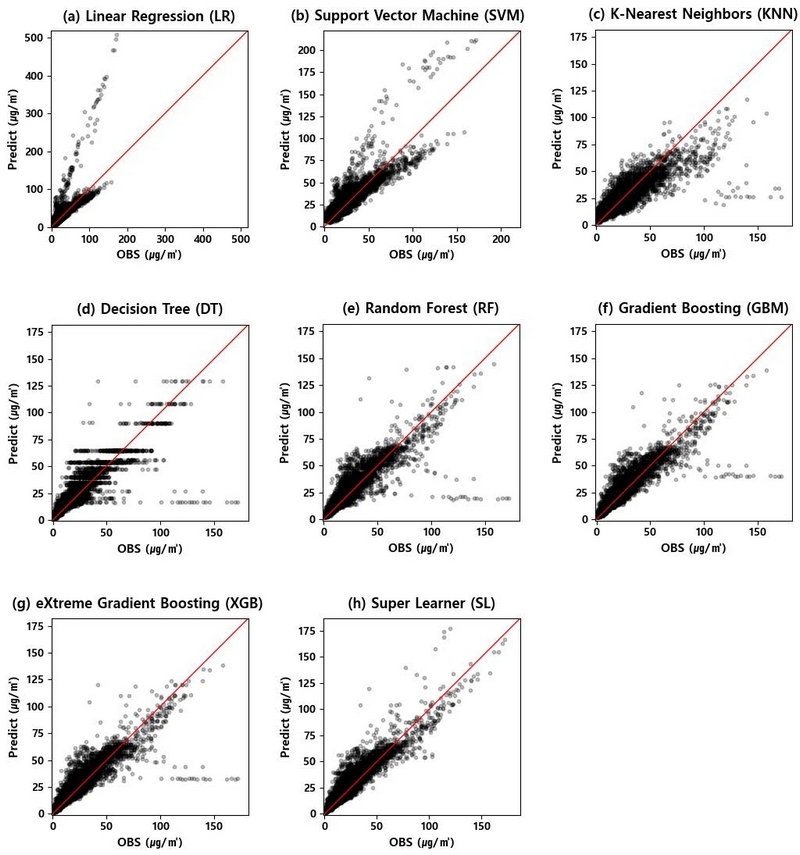
Scatter plots of the PM2.5 observations and the predicted PM2.5 values of each of the seven base learners and the Super Learner.

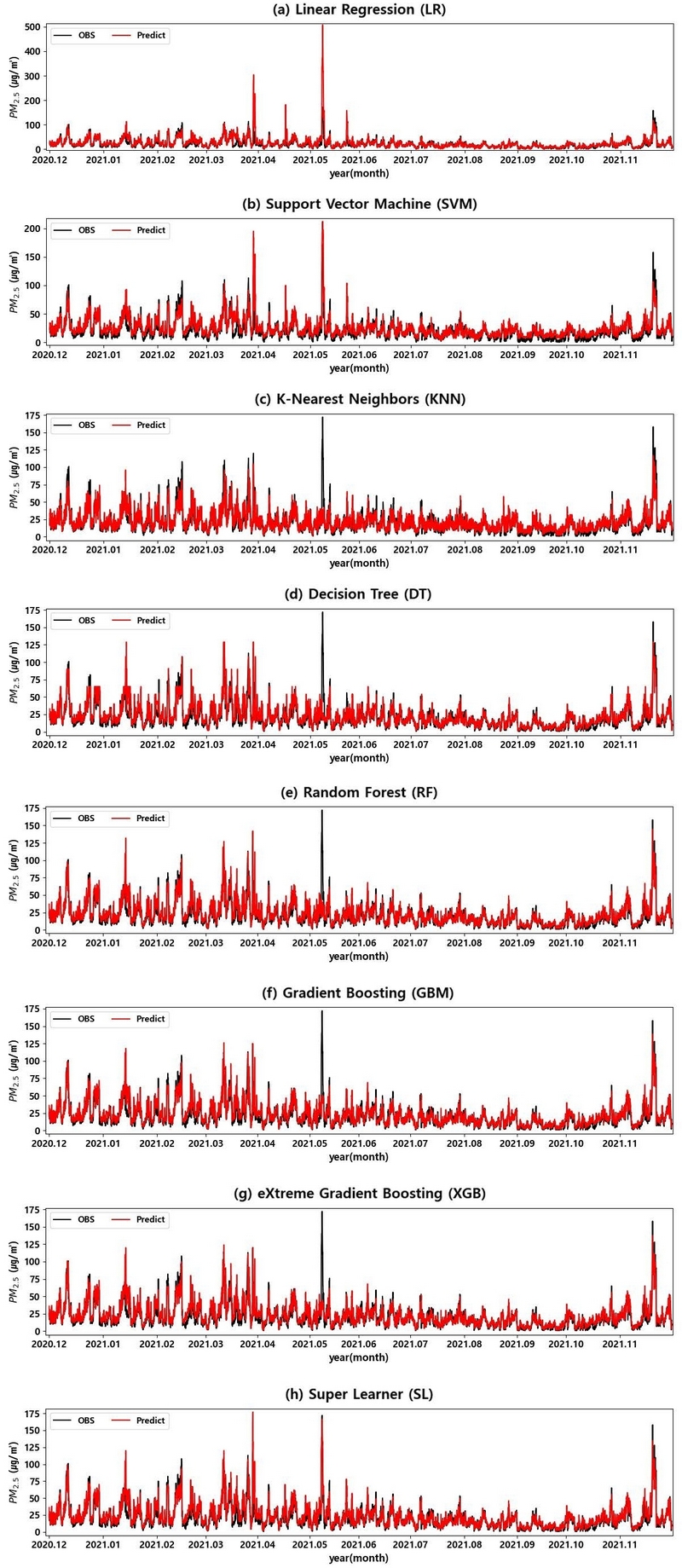
그림 5는 검증 기간에 대하여 관측된 PM_2.5 농도와 각 방법의 예측 농도를 나타낸 시계열 그래프이다. 대부분의 기저 학습기가 대체로 추세를 잘 따라가고 있지만, 고농도 관측치에 대해 서로 다른 결과를 보였다. 선형회귀 (LR)와 Support Vector Machine (SVM) (그림 5(a), (b))은 2021년 5월에 관측된 170 μg/m³ 이상의 고농도 관측치를 각각 500 μg/m³, 200 μg/m³으로 크게 예측하였다. 그 외 K-Nearest Neighbors (KNN), Decision Tree (DT), Random Forest (RF), Gradient Boosting (GBM), eXtreme Gradient Boosting (XGB) (그림 5(c), (d), (e), (f), (g))의 전체적인 예측 패턴은 선형회귀 (LR) 및 Support Vector Machine (SVM)과 비슷하지만 2021년 5월에 관측된 고농도에 대해서는 약 60 μg/m³ 이하의 값으로 예측하여 상대적으로 과소추정하고 있음을 볼 수 있다. 반면, 기저 학습기들의 예측을 가중 결합한 Super Learner (SL) (그림 5(h))는 2021년 3월 말에 관측된 값에 대해 크게 예측하였으며, 특히 2021년 5월에 발생한 고농도 관측치는 다른 기저 학습기에 비해 매우 유사하게 예측하고 있다. 즉, Super Learner는 다양한 기저 학습기로부터 생성된 예측치들의 가중 결합을 통해 새로운 예측을 제공하기 때문에 안정적이면서 이전에 학습하지 않은 새로운 값에 대해 강력한 예측을 제공하는 모델임을 알 수 있다. 또한, Super Learner를 구성할 때, 비슷한 종류의 기저 학습기보다는 서로 보완할 수 있는 다양한 종류의 알고리즘을 조합하는 것이 중요하다.

Fig. 5.

Time series plots of the PM2.5 observations (black lines) and the predicted PM2.5 values (red lines) from each of the seven base learners and the Super Learner.

4. 결 론

본 연구에서는 대기 오염 물질 자료를 기반으로 서울시 중구의 시간당 PM_2.5 농도를 예측하기 위해 여러 가지 기계학습 기법을 적용하고 이들의 예측 성능을 비교하였다. 기계학습 기법으로는 선형회귀, Support Vector Machine, K-Nearest Neighbors, Decision Tree, Random Forest, Gradient Boosting, eXtreme Gradient Boosting를 적용하였으며, 이들을 기저 학습기로 하여 최적의 조합을 찾는 Super Learner를 적용하였다. 추정된 기저 학습기의 가중치에 의하면 Random Forest와 eXtreme Gradient Boosting 및 선형회귀가 Super Learner 예측에 가장 큰 영향을 준 것으로 나타났다. 수집된 데이터 중 2년간의 데이터를 학습하여 이후 1년의 PM_2.5 농도를 예측한 결과, 모든 모델이 추세는 잘 예측하였지만 고농도 관측치에서 서로 다른 결과를 보였다. 기저 학습기 중 선형회귀와 Support Vector Machine은 검증 기간에 존재하는 고농도 관측치를 높게 예측하였으며, 그 외 앙상블 기법은 작게 예측하는 경향을 보였다. 반면, Super Learner는 고농도 관측치를 가장 정확하게 예측하였으며 기저 학습기에 비해 향상된 예측 결과를 보였다.

연구 결과를 통해 단일 모델보다는 앙상블 모델의 예측 성능이 우수함을 확인하였다. 특히, Super Learner는 여러 모델의 예측을 가중 결합함으로써 일반화 능력을 향상시키고 예측 오차를 줄여 기저 학습기보다 예측 성능이 향상된 결과를 보였다. 그러나, Super Learner는 기저 학습기들의 가중 결합으로 이루어지기 때문에 각 기저 학습기의 가중치를 어떻게 결정하는가에 따라 예측력이 달라질 수 있으므로 가중치 추정 방법에 대한 추가적인 연구가 필요하다. 또한, 본 연구에서는 시간당 대기 자료를 독립적인 샘플로 가정하여 분석하였지만 대기 관측 값은 이전 시간의 관측 값이나 지속 시간 등의 영향을 받을 수 있다. 특히, PM_2.5는 대기 오염 물질 뿐만 아니라 풍속, 습도, 강수 등 기상 변수의 영향도 받을 수 있기 때문에 기상 관측 자료와 시간 정보의 활용을 통해 더욱 정확한 예측이 가능할 것으로 보인다.

References

• Bae, H.-J. (2014) Effects of short-term exposure to PM₁₀ and PM_2.5 on mortality in Seoul, Journal of Environmental Health Sciences, 40(5), 346-354, (in Korean with English abstract). [https://doi.org/10.5668/JEHS.2014.40.5.346]
• Brieman, L. (1996) Bagging predictors, Machine Learning, 24, 123-140. [https://doi.org/10.1007/BF00058655]
• Breiman, L. (2001) Random forests, Machine Learning, 45, 5-32. [https://doi.org/10.1023/A:1010933404324]
• Chen, T., Guestrin, C. (2016) Xgboost: A scalable tree boosting system, In Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining, 785-794. [https://doi.org/10.1145/2939672.2939785]
• Danesh Yazdi, M., Kuang, Z., Dimakopoulou, K., Barratt, B., Suel, E., Amini, H., Lyapustin, A., Katsouyanni, K., Schwartz, J. (2020) Predicting Fine Particulate Matter (PM_2.5) in the Greater London Area: An Ensemble Approach using Machine Learning Methods, Remote Sensing, 12(6), 914. [https://doi.org/10.3390/rs12060914]
• Kim, H. (2020) The prediction of PM_2.5 in Seoul through XGBoost ensemble, Journal of the Korean Data Analysis Society, 22(4), 1661-1671, (in Korean with English abstract). [https://doi.org/10.37727/jkdas.2020.22.4.1661]
• Kim, H.-L., Moon, T.-H. (2021) Machine learning-based fine dust prediction model using meteorological data and fine dust data, Journal of the Korean Association of Geographic Information Studies, 24(1), 92-111, (in Korean with English abstract). [https://doi.org/10.11108/kagis.2021.24.1.092]
• Kim, M.-W., Jeong, H.-S. (2022) Development of machine learning based prediction of particulate matter concentration in Seoul, Journal of the Korean Data and Information Science Society, 33(6), 1095-1111, (in Korean with English abstract). [https://doi.org/10.7465/jkdi.2022.33.6.1095]
• Lee, D.-W., Lee, S.-W. (2020) Hourly prediction of particulate matter (PM_2.5) concentration using time series data and random forest, KIPS Transactions on Software and Data Engineering, 9(4), 129-136, (in Korean with English abstract). [https://doi.org/10.3745/KTSDE.2020.9.4.129]
• Ministry of Environment (ME) (2016) What is find dust?, Republic of Korea’s Ministry of Environment.
• National Institute of Environmental Research (NIER) (2022) Air Environment Annual Report.
• Park, H.-J. (2021) Analysis and prediction of (ultra) air pollution based on meteorological data and atmospheric Environment data, The Journal of Korea Institute of Information, Electronics, and Communication Technology, 14(4), 328-337, (in Korean with English abstract). [https://doi.org/10.17661/jkiiect.2021.14.4.328]
• Park, S.-H., Kim, M.-A., Im, J.-H. (2021) Estimation of ground-level PM₁₀ and PM_2.5 concentrations using boosting-based machine learning from satellite and numerical weather prediction data, Korean Journal of Remote Sensing, 37(2), 321-335, (in Korean with English abstract). [https://doi.org/10.7780/kjrs.2021.37.2.11]
• Polley, E.C., Van der Laan, M.J. (2010) Super learner in prediction. https://biostats.bepress.com/ucbbiostat/paper266
• Van der Laan, M.J., Polley, E.C., Hubbard, A.E. (2007) Super learner, Statistical Applications in Genetics and Molecular Biology, 6(1), 1-21. [https://doi.org/10.2202/1544-6115.1309]
• Wolpert, D.H. (1992) Stacked generalization, Neural Networks, 5(2), 241-259. [https://doi.org/10.1016/S0893-6080(05)80023-1]
• Zhai, B., Chen, J. (2018) Development of a stacked ensemble model for forecasting and analyzing daily average PM_2.5 concentrations in Beijing, China, Science of the Total Environment, 635, 644-658. [https://doi.org/10.1016/j.scitotenv.2018.04.040]