미세먼지 농도 예측을 위한 머신러닝 기법의 정확도 분석
Abstract
In this study, machine learning technique was applied by using PM10, PM2.5 and air quality data acquired from Urban Air Monitoring Network and Meteorological data acquired from Automated Synoptic Observing System (ASOS) and Aerosol Optical Depth (AOD), Ångström Exponent (AE) data acquired from the ground-based Sun-sky radiometer (AERONET) observation network or Satellite data (MODIS). For the determination of the best machine learning (ML) model, four ML techniques such as Multi Linear Regression (MLR), Support Vector Machine (SVM), Random Forest (RF), Deep Neural Network (DNN) were tested and compared accuracy using Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), R2, Mean Absolute Percentage Error (MAPE). Since the error range can be presented according to the diversity and variability of input data and ML, it is possible to compare the prediction accuracy of each model or determine the optimal prediction model. We also proved the assumption that more accurate results can be obtained by the optimized ML technique having the lowest error rate. The results showed that optimized ML model has the accuracy of 81.27% for PM10 concentration prediction and 73.25% for PM2.5 concentration prediction. It is expected that expanded air quality information through the using of ML based PM concentration prediction with the remote sensing data.
Keywords:
Aerosol, Particle matter, Air quality, Machine learning, Error analysis1. 서 론
대기 중 다양한 형태로 존재하는 에어로솔 (Aerosol) 입자는 대기 중에서 태양광을 흡수하거나 산란하며, 지구 복사 수지, 물 순환 및 기후 변화 과정에 직간접인 영향을 미친다 (IPCC, 2022; Charlson et al., 1992). 에어로솔의 한 부분으로, 대기 중의 입자상 물질 (Particulate matter, PM)인 미세먼지는 대기 중 고체 및 액적 상태 입자 형태의 혼합물로 배출되거나, 자연적 또는 화학적 반응으로 인해 생성되며, 주로 탄소, 이온, 광물 성분 등으로 구성되어 있는 것으로 알려져 있다 (NIER, 2021). 미세먼지 중 직경 2.5 마이크로미터 미만의 초 미세먼지 (PM2.5)는 입자의 크기가 매우 작아 폐 깊숙이 침투하여 호흡기 및 심혈관 질환을 일으킬 수 있으며 (Adar et al., 2014; Atkinson et al., 2014), 이보다 큰 직경 10 마이크로미터 미만의 미세먼지 (PM10)는 또한 호흡기 문제를 일으키고 가시거리 감소에 기여할 수 있다 (Lee et al., 2014). 또한 미세먼지는 생태계, 작물 및 기후에 부정적인 영향을 미칠 수도 있다. 전 세계적으로, 이러한 미세먼지에 의한 영향을 심각한 환경 문제로 인식하고 있으며, 대기질 관측 네트워크를 구축하여 실시간 대기질을 관측하고 예측 정보를 제공하고 있다.
국내에서는 1995년과 2015년부터 PM10과 PM2.5의 관측이 시작되었으며 (NIER, 2021), 이 중 PM10 농도는 최근까지 꾸준히 감소 추세에 있으며 사회적인 관심도도 급격하게 증가하였다 (Lee and Bae, 2021). 미세먼지에 대한 피해를 사전에 예방하기 위해 미세먼지 예보시스템에 관한 연구가 진행되었다. KIEST (2007)는 기상예보모델인 Fifth-Generation Penn State/NCAR Mesoscale Model (MM5)과 대기질 모델 Community Multiscale Air Quality Model (CMAQ)을 결합하여 한반도 대기질 수치예보모델을 구축한 결과, 서울 지역을 대상으로 전일 미세먼지 예보 결과는 정확도 71.76%, 당일 예보 결과는 정확도 85.39%로 나타났다. 또한, 지상 및 위성 데이터를 사용한 원격 관측 기법은 미세먼지 농도의 시공간적 변동성에 대한 정보를 제공할 수 있으므로, 많은 대기질 모니터링과 응용연구에 널리 사용되고 있다 (Lee et al., 2022; Lee and Shin, 2022; Li et al., 2021; Wei et al., 2020; Lee and Kim, 2010).
최근에는 인공지능 관련기술이 급격하게 발전하면서 머신러닝 및 딥러닝 기법을 이용한 대기오염물질의 농도를 예측하는 연구가 진행되고 있다 (Kim et al., 2022a). 예를 들어, Jeon and Son (2018)의 연구에서는 국내 주요 대도시 6개 지점 (서울, 부산, 인천, 대전, 광주, 대구)을 대상으로 대기질 자료와 기상자료를 머신러닝 기법에 적용하여 미세먼지 농도를 예측한 결과, 대구 지역에서는 예측 정확도가 78%, 광주 지역에서는 예측 정확도가 67%로 지역별 차이를 보고하였다. Cho et al. (2019)의 연구에서는 심층신경망 기법을 이용한 대기질을 예측 결과와 수치예측 모델링과 비교한 결과, PM10의 경우 약 75~85% 일치한다고 보고하였다. 서울 지역의 지상관측자료와 머신러닝 기법을 이용하여 PM 농도를 예측한 결과는 R2 값이 0.772~0.929 값 정도의 수준을 보였고 (Son and Kim, 2020), 하이브리드 머신러닝 모델이 적용된 결과는 기존의 예측 모델보다 더 나은 결과가 나타남을 확인하였다 (Yang et al., 2020). 이러한 결과는 해외에서도 유사한 사례가 보고되었다. Song et al. (2021)이 중국 전역에 대한 기상자료와 위성자료를 이용한 다양한 머신러닝 기법에 적용하여 PM2.5 농도를 예측한 결과, 독립적인 모델의 사용보다는 하이브리드 모델을 적용하였을 때 R2=0.84, RMSE=12.921로서 정확도가 가장 높게 나타남을 보였다.
따라서, 본 연구는 국내 주요 도시에서 관측된 지상관측자료와 컬럼 에어로솔 관측자료를 입력자료로 이용하는 최적의 머신러닝 기반의 미세먼지 예측값의 정확도 검증을 연구목표로 설정하였다. 이를 위하여 머신러닝 기법에 대한 학습 (training)과 시험 (test)한 결과에 대한 오차 분석을 수행하였다. 사용된 머신러닝 기법은 Multi Linear Regression (MLR), Support Vector Machine (SVM), Random Forest (RF), Deep Neural Network (DNN)으로서 개별 오차분석과정을 통하여 관측지점별 최적의 대기질 예측 모델을 선정하였다. 이렇게 선정된 최적의 머신러닝 기법을 이용하여 미세먼지 농도 예측값과 실제 관측자료와의 비교검증 과정을 통하여 머신러닝 기반의 대기질 예측 결과에 대한 정확도를 제시하였다.
2. 자료 및 방법
2. 1 연구 범위
연구 대상 지역은 대한민국에 위치한 지상 선포토미터 (Sun-photometer) 관측 네트워크인 Aerosol Robotic Network (AERONET), 환경부 도시대기측정망, 기상청의 자동기상관측망 (Automated Synoptic Observing System, ASOS)의 세 가지 관측지점이 반경 10 km 이내 존재하며, 2015년부터 2019년까지 자료가 존재하는 세 개의 관측지점인 강릉 (Gangneung_WNU, 37.771°N, 128.867°E, 60 m agl.), 광주 (Gwangju_GIST, 35.228°N, 126.843°E, 52 m agl.), 서울 (Yonsei_University, 37.564°N, 126.935°E, 97 m agl.)과 대표적인 미세먼지 고농도지역인 춘천 (Chuncheon, 37.876°N, 127.721°E agl.)과 원주 (Wonju, 37.352°N, 127.948°E agl.)를 포함한다 (그림 1). 서울과 광주는 대도시 지역이며, 강릉은 산지와 해양의 영향을 받는 복합지역, 원주와 춘천은 내륙 분지성 지역이다. 본 연구에서 사용된 머신러닝 기법에 사용된 입력자료는 Aerosol Optical Depth (AOD), Ångström Exponent (AE), SO2, NO2, O3, CO, PM10, PM2.5, 기온, 풍속, 풍향, 상대습도, 대기압, 가시거리, 이슬점이다.
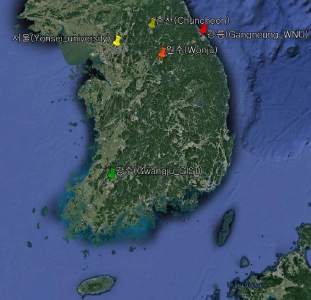
Geographic locations of measurement sites used in this study (Gangneung (37.771°N, 128.867°E, 60 m agl.), Gwangju (35.228°N, 126.843°E, 52 m agl.), Seoul (37.564°N, 126.935°E, 97 m agl.), Chuncheon (37.876°N, 127.721°E agl.), Wonju (37.352°N, 127.948°E agl.)).
머신러닝 기법에 사용된 입력자료 중 AOD, AE는 강릉, 광주, 서울에서는 AERONET 관측자료를 이용하였으며, 춘천과 원주 지점은 지구관측 인공위성인 Moderate Resolution Imaging Spectroradiometer (MODIS) Level 2 aerosol 산출물 자료를 이용하였다. MODIS 위성관측자료와 지상의 Sun-photometer 관측자료는 구름이나 외부 요인 등으로 인한 비정상적인 자료들을 제거하여 산출된 Level 2.0 자료이다. 이러한 자료들은 MODIS 위성자료 데이터 베이스 (https://ladsweb.modaps.eosdis.nasa.gov/)와 AERONET 데이터베이스 (https://aeronet.gsfc.nasa.gov/)로부터 획득하였다. 국내 대기질 관측자료는 Airkorea (https://www.airkorea.or.kr/), 기상관측자료는 기상자료개방포털 (https://data.kma.go.kr/)에서 수집하였다. 자세한 관측지점별 기간과 목록에 대한 상세 설명은 표 1과 같다.
2. 2 지상관측자료
본 연구에서 사용된 지상관측자료는 미세먼지 농도와 컬럼 에어로솔 그리고 기상관측자료이다. 미세먼지 농도는 국내 도시대기측정망에서 측정된 PM10과 PM2.5 중량농도로서, 자동 관측기에 의하여 베타선법 (β-Ray Absorption Method)으로 관측된 결과이다 (NIER, 2021). 베타선법을 통한 미세먼지 농도 계산은 일정기간 동안 필터에 포집된 먼지층을 베타선이 투과할 때 변하는 베타선량을 측정하여 식 (1)과 식 (2)로부터 농도값으로 환산한다 (Choi et al., 2018).
| (1) |
식 (1)에서 I는 필터에 채취된 먼지를 투과한 베타선의 강도, I0는 먼지가 채취되지 않은 필터에 투과된 베타선 강도, μ는 미세먼지에 의한 흡수 소멸계수 (cm3/mg), X는 포집된 미세먼지의 질량밀도 (mg/cm3)이다. 식 (1)을 통해 계산된 I 값을 식 (2)에 적용하면 미세먼지 농도를 계산할 수 있다.
| (2) |
식 (2)에서 C는 미세먼지 농도 (μg/m3), S는 채취한 여과지의 면적 (m2), Q는 흡입된 공기유량 (m3), Δt는 샘플링 시간 (minute)을 나타낸다.
컬럼 에어로솔은 지표면에서 대기상층부까지 연직방향에 존재하는 모든 입자상 물질에 대한 부하량을 의미한다. 컬럼 에어로솔을 관측하는 대표적인 관측장비는 분광광도계로서 지구로 입사하는 태양광이 대기중에서 감쇄된 양으로부터 컬럼 에어로솔의 양을 간접적으로 측정한다. 본 연구에서 사용된 분광광도계는 CE-318 Sun-photometer (Model: CE-318, CIMEL Electronique, France, https://www.cimel.fr/solutions/ce318-t/) 이며, 이 장비는 8개의 중심 파장 대역에서 (340 nm, 380 nm, 440 nm, 500 nm, 675 nm, 870 nm, 939 nm 및 1,020 nm)에서 직사광 또는 산란광을 측정하는 다중 파장 분광광도계이다. CE-318 Sun-photometer는 대기 질량 (air mass)이 7 미만인 낮 동안 지표에 도달하는 직사광을 측정한다. 여기서 대기 질량은 태양고도각의 코사인 함수의 역수값으로 표현되므로 태양이 연직방향에 있는 경우 1의 값을 가지며 태양이 지평선에 가까워질수록 커지는 값을 가진다. 측정된 직사광으로부터 미량 기체의 흡수에 의한 투과도 및 레일리 산란 (Rayleigh Scattering)을 보정을 한 후, 식 (3), 식 (4)와 같이 Beer-Bouguer 법칙을 이용하여 AOD를 산출한다 (Giles et al., 2019). AOD는 대기 컬럼 내에 존재하는 모든 입자성 물질의 총 부하량을 상대적으로 나타낸 수치로서 각 고도별 에어로솔의 소산계수의 합과 같다.
| (3) |
| (4) |
식 (3)에서 V(λ)는 파장에 의존하는 계측기에서 측정된 전압, V0(λ)는 파장에 의존하는 보정 계수이며, d는 태양-지구 거리에 대한 평균비율 (Michalsky, 1988), τtotal(λ)는 총 광학 두께, m은 대기의 광경로 (Kasten and Young, 1989)이다. 식 (4)에서 τaerosol(λ)는 에어로솔 광학 두께, τRayleigh(λ)는 레일리 산란에 의한 광학 두께이며, τgas(λ)는 가스성 물질 흡수에 의한 광학 두께이다.
2. 3 위성관측자료
본 연구에서 사용한 위성자료는 National Aeronautics and Space Administration (NASA)의 지구관측 위성인 EOS-Terra 위성에 탑재된 MODIS 센서로부터 생산되는 에어로솔 표준 자료인 MOD04 자료를 이용하였다. MOD04는 10 km × 10 km 해상도로 전 지구적인 에어로솔의 광학적, 물리학적 파라미터와 분포를 포함하는 MODIS Aerosol Product로서 육지 및 해양에서 AOD와 AE 등 Aerosol과 관련된 자료를 포함하고 있다. MODIS는 AOD 생성을 위해 해양과 육지에서 각각 다른 알고리즘을 사용하여 AOD를 산출한다. 육지와 해양에서의 지표반사도의 광학 특성을 고려하여 지표면 반사도를 산출한 후, 위성이 관측한 복사량으로부터 보정하여 대기에 의한 신호를 분리한다 (Kaufman et al., 1997b). 그리고 대기에 의한 신호는 미리 계산된 조견표 (Look Up Table, LUT)를 적용하여 AOD를 산출한다 (Kaufman et al., 1997a; Tanré et al., 1997). 이렇게 산출한 AOD의 오차는 0.05±0.2로 알려져 있다 (Kaufman et al., 1997a).
2. 4 머신러닝 기법
연구 대상 지역 최적의 PM10, PM2.5 예측 모델을 구축 및 평가하기 위하여 머신러닝 기법으로 널리 사용되고 있는 SVM, RF, MLR, DNN 기법을 사용하였다. 이 중 각 관측지점별 최적의 예측 모델을 적용하기 위해 각 머신러닝 기법의 오차범위를 평가하였으며, 예측한 PM10, PM2.5 값과 실제 관측값을 비교하여 모델의 정확도를 비교 및 검증하였다. 본 연구의 자료처리흐름도는 그림 2와 같으며, 각각의 머신러닝 툴은 오픈소스 패키지인 R과 라이브러리를 사용하였다. 각각의 머신러닝 기법에 대한 상세한 설명은 다음과 같다.
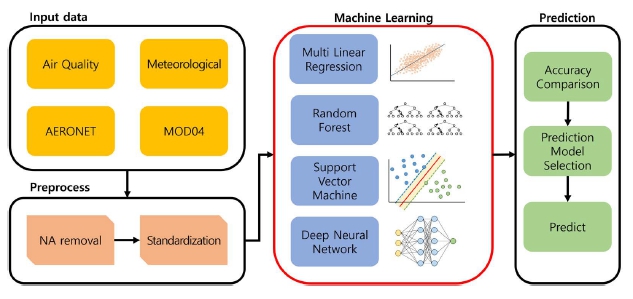
Flowchart of data processing used in this study. Four components are involved, collecting input data, preprocessing of dataset for machine learning estimation, independent machine learning techniques for error analysis, and PM concentration prediction, respectively.
첫 번째로, MRL은 종속변수에 영향을 미치는 요인이 여러 개가 존재할 때, 각각의 독립변수에 대한 기여도가 선형적으로 의존하는 것을 가정한다. MRL에서 사용되는 다중 선형 회귀 방정식은 식 (5)와 같이 한 개의 종속변수 (Y)와 여러 개의 독립변수 (Xi)가 존재한다.
| (5) |
위 식에서 a0는 상수, a1…an은 회귀계수, ε는 오차를 의미한다. 본 연구에서 사용된 MRL 모델의 종속변수는 PM10, PM2.5, 독립변수는 대기오염물질, 기상자료 및 컬럼 에어로솔 자료로 설정하였다.
두 번째 사용된 RF 기법은 예측을 위해 여러 개의 의사 결정 트리 (Decision Tree)를 사용하는 앙상블 기계 학습 알고리즘이다. 개별 트리를 사용하는 방법보다 더 정확한 예측을 생성하기 위해 여러 개의 의사 결정 트리를 결합하며, 각 결정 트리는 임의로 선택된 데이터 하위 집합에 대해 학습된다. 최종 결과에 대한 예측은 모든 결정 트리의 예측에 대한 평균 또는 다수결 투표를 통해 이루어지므로, 통계적인 유의성을 확보하게 된다. 또한, RF는 분류 및 회귀 작업 모두에 사용되며 데이터의 비선형 관계를 처리할 수 있고, 과적합 문제가 발생하지 않는 특징으로 인하여 정확한 예측을 생성하기 위한 강력한 기계 학습 알고리즘이다. 그러나, RF 기법은 데이터의 양이 많은 경우에도 비교적 처리 속도가 빠르고 변수 간의 비선형성을 잘 반영한다는 장점이 있지만, 결과 해석이 어려운 단점이 존재한다 (Breiman, 2001).
세 번째 사용된 SVM 기법은 분류 및 회귀 분석에 널리 사용되는 감독 머신러닝 알고리즘이다. SVM은 데이터 분석, 자료 분석 및 패턴 인식 등을 위하여 각 데이터를 구분할 수 있는 고차원 공간에서 초평면을 찾는 원리로 작동하며, 이 초평면은 초평면과 가장 가까운 데이터 포인트 사이의 거리가 최대화되는 방식으로 선택된다. 이러한 방법은 각 집단에 대한 경험적 오류를 최소화하는 의사결정함수를 사용하여 비교적 정확도가 높은 것으로 알려져 있으며, 선형과 비선형 데이터 모두 분석이 가능한 장점이 있다 (Cortes and Vapnik, 1995).
마지막으로, DNN은 상호 연결된 여러 계층의 노드가 있는 인공 신경망으로 구성되어 있으며, 데이터의 복잡한 관계를 모델링할 수 있다. DNN은 인간 두뇌의 구조와 기능을 모사하여 개발되었으며, 대용량의 데이터를 학습하여 예측과 분류 작업을 수행할 수 있다. DNN의 각 노드는 수신한 입력값을 처리하고 다음 계층으로 전달하는 과정을 반복함으로써, 더 복잡한 데이터 표현을 구축할 수 있다. DNN의 학습 과정에서는 네트워크를 통한 예측값이 실제값에 최대한 근접하도록 각 노드의 가중치와 편향을 조정하는 작업을 수행한다. 이는 역전파 (backpropagation) 프로세스를 통하여 오차를 줄이는 방식으로 가중치와 편향을 업데이트하는 데 사용된다 (Cho et al., 2018). DNN은 데이터 학습을 통하여 예측하고 복잡한 작업을 수행할 수 있는 강력한 인공 신경망 기법이지만, 학습에 소요되는 시간이 오래 걸리는 단점이 있다 (Kim et al., 2019).
3. 결과 및 토의
3. 1 미세먼지 농도 현황
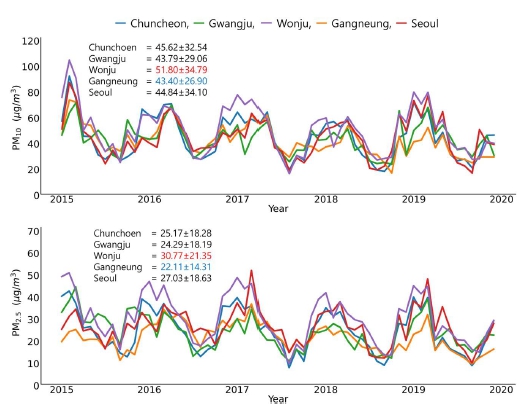
그림 1에서 제시된 5개 관측지점의 미세먼지 농도의 현황 및 변화 특성을 이해하기 위하여 각 관측지 점별 PM10, PM2.5 농도자료에 대한 기술 통계 분석 을 수행하였다. 그림 3은 2015년부터 2019년까지 관측된 월평균 PM10, PM2.5 농도값의 시계열 변화이다. 해당 기간 동안의 각 관측지점별 평균 PM10 농도는 51.80±34.79 µg/m3 (원주), 45.62±32.54 µg/m3 (춘천), 44.84±34.10 µg/m3 (서울), 43.79±29.06 µg/m3 (광주), 43.40±26.90 µg/m3 (강릉)의 순서대로 큰 값이 관측되었다. 또한, 각 지점별 평균 PM2.5 농도는 30.77±21.35 µg/m3 (원주), 27.03±18.63 µg/m3 (서울), 25.17±18.28 µg/m3 (춘천), 24.29±18.19 µg/m3 (광주), 22.11±14.31 µg/m3 (강릉)의 순서로 나타났다. 각 지역별 시계열 변화 경향은 대체적으로 겨울철에 PM 농도가 높아지고 여름철에 낮아지는 계절별 변화를 확인할 수 있다. 이러한 계절별 변동성이 나타나는 원인으로는 봄철의 황사 현상, 여름철의 강수로 인한 세정효과, 겨울철 난방에 의한 화석연료의 연소 배출의 증가 등이 주요 원인으로 알려져 있다 (NIER, 2021).
3. 2 머신러닝 기법의 성능 평가
각 관측지점에서 PM 농도 예측 성능을 평가하기 위하여 SVM, RF, MLR, DNN 기법을 적용하여 모델의 학습과 학습된 결과를 토대로 예측한 결과를 비교하였다. 이러한 방법은 머신러닝을 이용한 예측에 앞서 입력자료에 대한 다양성과 변동성이 모델링 방법론에 따라 오차수준 범위를 제시할 수 있으므로 모델별 예측 정확도를 비교하거나 최적의 예측 모델을 결정할 수 있다. 머신러닝 기법을 이용한 예측값을 평가하기 위하여 사용된 오차범위 지표는 평균 절대 오차 (Mean Absolute Error, MAE), 평균 제곱근 오차 (Root Mean Squared Error, RMSE), 평균 절대 백분율 오차 (Mean Absolute Percentage Error, MAPE)와 예측값과 관측값의 상관관계를 평가하기 위한 결정계수 (coefficient of determination, R2)를 사용하여 평가하였다. MAE는 n개의 데이터 예측값()과 관측값(yi)의 평균 편차이며 (식 (6)), 절대 오차에 대한 선형적인 관계를 표현할 수 있다. MAE 가 낮은 값은 더 정확한 모델을 의미한다.
| (6) |
RMSE는 식 (7)과 같이 오차의 제곱값에 대한 평균이므로 MAE보다 이상값에 더 민감하고, 낮은 값일수록 더 정확한 모델을 나타낸다.
| (7) |
MAPE는 관측값과 예측값 사이의 백분율 오차의 절대값에 대한 평균값이며 (식 (8)), 낮은 값일수록 더욱 정확한 모델 결과를 나타낸다. MAPE는 데이터의 비교 시점 간에 값이 크게 다르고 이상값이 큰 영향을 미치는 경우에 유용하게 사용된다.
| (8) |
R2은 식 (9)와 같이 두 값에 대한 회귀분석모델이 얼마나 데이터를 잘 설명해주는지를 나타내는 값으로서, 0~1 사이의 범위를 가진다.
| (9) |
즉, 오차범위를 설명해주는 MAE, RMSE, MAPE는 값이 작을수록 예측 오차가 적은 것을 의미하고, R2은 1에 가까운 값일수록 두 변수 간의 정확도가 높으며, 값이 작을수록 정확도가 낮은 것을 의미한다.
그림 4는 PM10 농도에 대해 관측지점별 입력자료를 개별 머신러닝 기법에 적용한 결과 중 지역별 가장 높은 정확도와 가장 낮은 정확도를 나타낸 사례를 비교한 결과이다. 예를 들어, 그림 4(a)에서 원주의 PM10은 DNN 모델의 예측 오차가 가장 낮았으며 (MAE=9.46 μg/m3, RMSE=13.21 μg/m3, MAPE=20.50%) 실제 관측값과의 비교에서 높은 상관관계 (R2=0.90)를 보였다. 이와는 상대적으로, 그림 4(b)에서는 원주의 PM10 농도를 MLR 모델로 예측한 경우에서 예측 오차가 가장 큰 결과 (MAE=11.07 μg/m3, RMSE=16.48 μg/m3, MAPE=21.85%)와 함께 낮은 상관관계 (R2=0.86)를 보였다. 이와 같은 방법으로 원주의 경우 DNN, 춘천 RF, 광주 RF, 강릉 RF, 서울 DNN 모델이 각각 오차범위 지수값과 상관관계가 가장 높은 결과를 나타냈다.
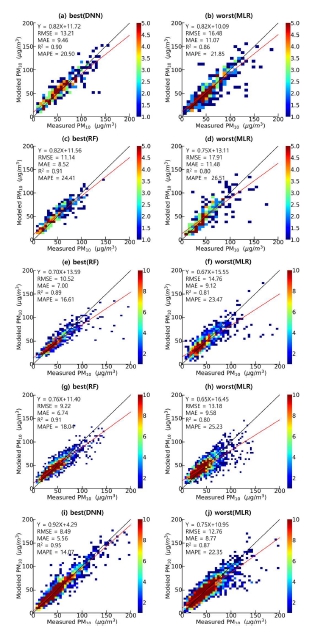
Scatterplots of model predicted and observed PM10 data in Wonju (a, b), Chuncheon (c, d), Gwangju (e, f), Gangneung (g, h), and Seoul (i, j) from top to bottom. The models with the best accuracy on the left and the worst on the right are also shown.
그림 5는 5개의 관측지점별 PM2.5 농도를 예측하기 위한 머신러닝 기법 중 가장 높은 정확도와 가장 낮은 정확도를 나타낸 결과를 비교한 사례이다. PM10 농도 예측의 경우와 마찬가지로 각 지역별로 오차범위 지수값과 결정계수값을 비교하였다. 그림 5(a)에서 원주의 PM10은 DNN 모델의 예측 오차가 가장 낮았으며 (MAE=9.46 μg/m3, RMSE=13.21 μg/m3, MAPE=20.50%), 실제 관측값과의 비교에서 높은 상관관계 (R2=0.90)를 보였다. 이와는 상대적으로, 그림 5(b)에서는 원주의 PM2.5 농도를 MLR 모델로 예측한 경우에서 예측 오차가 가장 큰 결과 (RMSE=16.48 µg/m3, MAE=11.07 µg/m3, MAPE=21.85%)와 함께 낮은 관계 (R2=0.86)를 보였다.
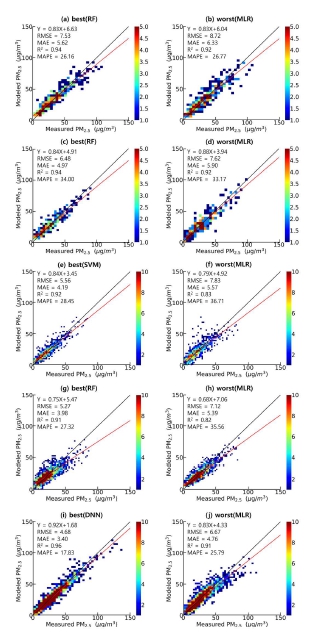
Scatterplots of model predicted and observed PM2.5 data in Wonju (a, b), Chuncheon (c, d), Gwangju (e, f), Gangneung (g, h), and Seoul (i, j) from top to bottom. The models with the best accuracy on the left and the worst on the right are also shown.
그림 6, 7은 PM10과 PM2.5 농도 예측을 위하여 SVM, RF, MLR, DNN 기법에 적용하여 생성된 결과에 대한 MAE, RMSE, MAPE, R2을 관측지점별로 비교한 결과이다. 대체적으로 서울의 PM10과 PM2.5 농도를 예측한 결과에 대한 오차범위는 다른 지역에 비하여 낮은 수준을 보였다. 서울의 PM10 예측 결과에 대한 오차범위와 다른 도시와의 평균적인 차이는 ΔMAE=-1.584 µg/m3, ΔRMSE=-1.978 µg/m3, ΔMAPE=-3.401%로 낮았으며, ΔR2=0.034로 다소 높은 수준의 상관관계를 가진다. 이와는 반대로 원주의 PM10 예측 결과에 대한 오차범위와 다른 도시와의 평균적인 차이는 상대적으로 크게 나타났으나 (ΔMAE=1.767 µg/m3, ΔRMSE=2.163 µg/m3, ΔMAPE=0.669%), 결정계수값은 서울에 이어 두 번째로 큰 값 (ΔR2=0.003)을 보였다. 서울의 PM2.5 예측 결과에 대한 오차범위와 다른 도시와의 평균적인 차이는 ΔMAE=-1.056 µg/m3, ΔRMSE=-1.181 µg/m3, ΔMAPE=-7.464%로 낮았으며, ΔR2=0.026으로 다른 도시 대비 높은 상관관계를 가진다. 오차범위가 가장 크게 나타나는 원주의 PM2.5 예측 결과에 대한 오차범위도 PM10의 경우와 마찬가지로 다른 도시대비 큰 오차범위 (ΔMAE=1.307 µg/m3, ΔRMSE=1.746 µg/m3, ΔMAPE=2.238%), 결정계수값은 서울에 이어 두 번째로 큰 값 (ΔR2=0.013)을 보였다.
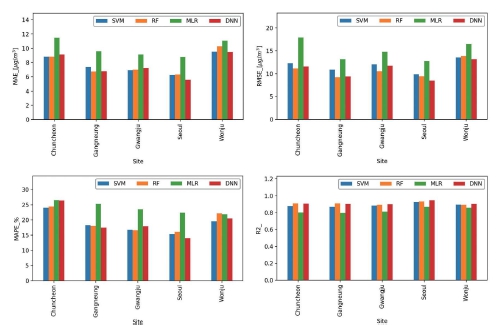
Comparisons of MAE, RMSE, MAPE, and R2 values for PM10 prediction by different machine learning techniques for each observation sites.
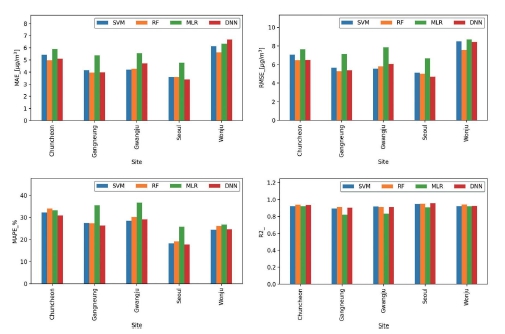
Comparisons of MAE, RMSE, MAPE, and R2 values for PM2.5 prediction by different machine learning techniques for each observation sites.
그리고 그림 6, 7의 결과에서는 네 가지 머신러닝 기법 중에서 MRL 기법은 다른 기법에 비하여 상대적으로 높은 오차범위와 낮은 결정계수값을 가지고 있는 것을 알 수 있다. 이는 입력자료로 사용되는 지상관측과 위성관측자료를 이용한 PM 농도 예측을 위한 머신러닝 기반의 모델링에 사용되는 방정식으로 사용되는 다중선형회귀 방정식의 사용에 있어 독립변수의 개별 기여도 및 변수 간의 관련성에 대한 해석에 한계가 있기 때문에 발생한 결과로 판단된다.
각 지역별 특징을 살펴보면, PM10과 PM2.5 모두 서울 지역의 관측자료를 DNN 모델에 적용하였을 때 가장 적은 오차지수 값의 범위를 나타냈고 (PM10: MAE=5.56 µg/m3, RMSE=8.488 µg/m3, MAPE=14.069%, PM2.5: MAE=3.40 µg/m3, RMSE=4.685 µg/m3, MAPE=17.833%), 가장 큰 결정계수값 (PM10: R2=0.947, PM2.5: R2=0.959)을 보임으로 인하여 각 사례 중에서 가장 높은 예측 정확도를 가짐을 알 수 있었다.
그림 6에서 서울을 제외한 나머지 지역의 개별 오차지수에 대해 살펴보면, 먼저 강릉의 PM10 농도의 예측을 위하여 RF 기법을 사용한 경우가 가장 낮은 오차범위 지수 MAE=6.74 µg/m3, RMSE=9.221 µg/m3, DNN 기법을 사용한 경우의 MAPE=17.481%와 RF 기법 을 사용한 경우에 가장 큰 결정계수 R2=0.909를 나타냈다. 광주의 PM10 농도의 예측 결과에 대하여 가장 낮은 오차범위 지수를 나타내는 기법은 SVM 기법을 적용한 경우의 MAE=6.95 µg/m3, RF 기법의 RMSE=10.523 µg/m3, RF 기법의 MAPE=16.787%이며, 가장 큰 결정계수는 DNN을 적용한 경우에서 R2=0.900을 나타냈다. 춘천의 PM10 농도의 예측을 위하여 RF 기법을 사용한 경우가 가장 낮은 오차범위 지수 MAE=8.82 µg/m3, RMSE=11.142 µg/m3, SVM 기법을 사용한 경우에서 MAPE=23.981%와 가장 큰 결정계수 는 RF 기법의 R2=0.908을 나타냈다. 원주의 PM10 농 도의 예측을 위하여 DNN 기법을 사용한 경우가 가장 낮은 오차범위 지수 MAE=9.46 µg/m3, RMSE=13.211 µg/m3, SVM 기법을 사용한 경우 MAPE=19.562%와 가장 큰 결정계수 R2=0.901을 나타냈다.
그림 7은 PM2.5 농도의 예측 결과에 대한 오차범위를 도시한 것으로서, 강릉의 PM2.5 농도의 예측을 위하여 RF 기법을 사용한 경우가 가장 낮은 오차범위 지수 MAE=3.96 µg/m3, RMSE=5.274 µg/m3, DNN 기법을 사용한 경우의 MAPE=26.330%, RF 기법을 사용한 경우에 가장 큰 결정계수 R2=0.911을 나타냈다. 광주의 PM2.5 농도의 예측 결과에 대하여 가장 낮은 오차범위 지수를 나타내는 기법은 SVM 기법을 적용한 경우의 MAE=4.19 µg/m3, RF 기법의 RMSE=5.561 µg/m3, MAPE=28.455%이며, 가장 큰 결정계수는 SVM을 적용한 경우에서 R2=0.917을 나타냈다. 춘천의 PM2.5 농도의 예측을 위하여 RF 기법을 사용한 경우가 가장 낮은 오차범위 지수 MAE=4.97 µg/m3, RMSE=6.476 µg/m3, DNN 기법을 사용한 경우에서 MAPE=30.879%, 가장 큰 결정계수는 RF 기법의 R2=0.937을 나타냈다. 원주의 PM2.5 농도의 예측을 위하여 RF 기법을 사용한 경우가 가장 낮은 오차범위 지수 MAE=5.62 µg/m3, RMSE=7.532 µg/m3, SVM 기법을 사용한 경우 MAPE=24.382%와 RF 기법에서 가장 큰 결정계수 R2=0.940을 나타냈다.
개별 머신러닝 기법을 적용하여 PM 농도를 예측한 결과에 대한 오차수준 분석 결과를 통하여 관측지점별로 오차율이 다르게 나타남을 알 수 있었다. 이러한 결과는 단순히 단일 예측 모델의 사용이 예측 오차를 줄일 수 있는 유일한 수단이 아님을 의미한다. 따라서, 본 연구에서는 개별 머신러닝 기법에 대한 최저 오차율을 가지는 기법을 최적의 모델로 선정하여 PM 농도를 예측한다면 보다 정확한 결과를 얻을 수 있다는 가정을 증명하였다. 또한, 보다 정량적인 방법론의 확보를 위하여, 개별 기법에 대한 오차범위 지수에 대한 상대평가를 수행하여 최고 등급을 획득한 모델을 최종적으로 선택하는 방법론을 사용하였다. 이러한 방법은 선행 연구를 통하여 지상관측자료의 예측에서 우수한 성능을 가짐을 확인하였다 (Kim et al., 2023).
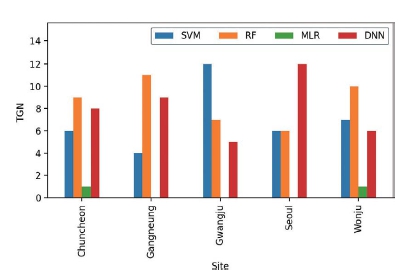
최적의 모델 선정을 위한 방법은 각 관측지점에서 여러 머신러닝 기법에 적용하여 나온 Test 결과에 대해 MAE, RMSE, MAPE, R2 값들에 대한 상대 등급을 A (3점), B (2점), C (1점), D (0점)과 같이 부과하여 총합 (Total Grade Number, TGN)이 가장 높은 기법을 선정하는 방법이 사용되었다. 그림 8에서는 TGN 값을 이용하여 각 관측지점에 대한 최적화 점수를 판단할 수 있으며, PM10의 경우는 서울과 원주에서 DNN 기법에 적용하였을 때 각각 12점과 11점으로 가장 높은 값을 보였다. 강릉, 광주, 춘천에서는 RF 기법이 가장 높은 TGN 값을 나타냈다. 그러나, 모든 지점에서 공통적으로 MLR 기법을 적용한 경우에는 0점이거나 최하점수를 나타내고 있으므로 최적 모델로 추천하기 어려운 결과를 보였다.
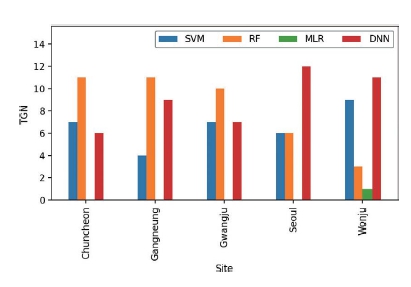
Comparisons of total grade number (TGN) values for PM10 prediction by different machine learning techniques for each observation sites.
그림 9는 동일한 방법으로 PM2.5에 대한 TGN 값을 비교한 결과이다. PM10의 경우와 다르게 춘천, 강릉, 원주에서는 RF 기법이 가장 큰 TGN 값을 나타내고 있고 (각각 9점, 11점, 10점), 광주는 SVM (12점), 서울은 DNN 기법 (12점)에 적용하였을 때 가장 큰 값을 보였다. MRL 기법은 PM10의 경우와 마찬가지로 모든 지점에서 최하점수를 나타내고 있으므로, PM 농도 예측을 위한 최적의 모델로 평가하기 어려운 것으로 판명되었다.
3. 3 PM 농도 예측 결과
이전 장에서 각 관측지점별로 선정된 최적의 예측 기법을 사용하여 예측한 PM 농도값과 실제 관측값의 비교 결과는 표 2, 3에 정리하였다. 표 2에서 각 지역별 PM10을 예측한 결과 결정계수는 모두 0.9 이상의 높은 상관성을 가지는 결과를 보였다. 각 지점에 대한 평 균 오차범위는 MAE=7.516±1.595 µg/m3, RMSE=10.516±1.832 µg/m3, MAPE=18.726±3.940%와 가장 큰 결정계수 R2=0.912±0.023의 범위를 나타냈다. 이러한 오차범위 수준은 표 2에서 제시된 다른 연구 결과 사례와 비교했을 때, 보다 낮은 수준의 오차범위와 높은 상관관계를 제시할 수 있음이 확인된다. 또한, MAPE 값으로부터 정확도 수치를 계산해보면 본 연구에서 PM10 농도를 예측한 결과는 약 81.27% 수준의 정확도를 가지는 것으로 판단된다.
표 3은 각 지역별 PM2.5를 예측한 결과에 대한 오차범위 수준과 타 연구 사례를 비교한 표이다. PM10의 경우와 마찬가지로 지역별 PM2.5 농도 예측 결과는 모두 결정계수 0.9 이상의 높은 상관성을 가지는 결과를 보였다. 각 지점에 대한 평균 오차범위는 MAE=4.428±0.873 µg/m3, RMSE=5.904±1.117 µg/m3, MAPE=26.752±5.824%와 결정계수 R2=0.934±0.019의 범위를 나타냈다. 이러한 오차범위 수준은 표 3에서 제시된 다른 연구 결과 사례와 비교했을 때, 보다 낮은 수준의 오차범위와 높은 상관관계를 제시할 수 있음이 확인된다. 또한, MAPE 값으로부터 정확도 수치를 계산해보면 본 연구에서 PM2.5 농도를 예측한 결과는 약 73.25% 수준의 정확도를 가지는 것으로 판단된다.
4. 요약 및 결론
미세먼지에 의한 영향은 파악하고 그로 인한 피해를 사전에 예방하기 위하여 수행되는 미세먼지 예측 활동은 매우 중요하다. 본 연구에서는 국내의 5개 주요 도시 관측지점 (강릉, 광주, 서울, 춘천, 원주)에서 관측된 대기질, 기상, 컬럼 에어로솔 자료를 이용하여 머신러닝 기법 중 MLR, RF, SVM, DNN에 적용 후 미세먼지 농도를 예측하였다. 지역별, 머신러닝 기법별 예측 결과에 대한 오차범위와 상관도를 분석하여 예측 성능을 평가하였으며, 다음과 같은 결론을 도출하였다.
첫째, 각 지역별로 개별 머신러닝 기법을 적용하여 미세먼지 농도를 예측한 결과는 모델에 따라 오차범위가 상이하였으며, 이는 입력자료의 특성 (예: 오염원, 기상학적 요인, 지형적 요인 등)과 머신러닝 기법에 사용되는 해석적 방법이 복잡하게 적용된 결과인 것으로 판단된다. 따라서, 미세먼지 농도 예측을 위한 머신러닝 기반의 모델을 구축할 때는 각 대상 지역에 대하여 단일 모델을 적용하는 것보다는 다양한 머신러닝 기법을 적용하여 결과 수치를 비교 평가하는 것이 필요함을 의미한다.
둘째, 개별 머신러닝 기법을 적용하여 PM 농도를 예측한 결과를 통하여 관측지점별로 오차율과 결정계수를 분석하였다. 이 값들은 최적의 머신러닝 기법을 선정하기 위한 TGN 평가에 사용하여 최적의 모델을 선정하였고, 각 지점별 오차율이 가장 낮고 상관도가 가장 높은 머신러닝 기법을 선택할 수 있는 방법론으로 제시하였다.
셋째, 지역별로 선택된 최적의 머신러닝 기법을 이용하여 미세먼지 농도를 예측한 결과에 대한 정확도 검증 결과, 예측된 PM10 농도의 평균 오차범위는 MAE=7.516±1.595 µg/m3, RMSE=10.516±1.832 µg/m3, MAPE=18.726±3.940% (정확도=약 81.27%), R2=0.912±0.023의 범위를 나타냈다. 예측된 PM2.5 농도의 평균 오차범위는 MAE=4.428±0.873 µg/m3, RMSE=5.904±1.117 µg/m3, MAPE=26.752±5.824% (정확도=약 73.25%), R2=0.934±0.019의 범위를 나타냈다. 이러한 오차범위 수준은 표 2, 3에서 제시된 다른 연구 결과 사례와 비교했을 때, 보다 낮은 수준의 오차범위와 높은 상관관계를 가지고 있는 것으로 확인되었다.
이러한 결과는, 본 연구에서 제시된 머신러닝 기법을 이용한 미세먼지 농도 산출을 위한 방법론과 PM10, PM2.5 농도 예측은 유효한 결과를 나타내고 있음을 의미한다. 본 연구의 접근 방법을 통하여 지상의 미세먼지 관측소가 존재하지 않는 지역이나 비접근 지역에서 원격탐사 자료에 적용하면, 미세먼지 농도 예측이 가능할 것으로 예상되므로 향후 활용 가능성이 높을 것으로 판단된다. 따라서, 본 연구의 빅데이터와 머신러닝 기법을 이용한 미세먼지 농도 예측을 통해 보다 더 정밀하고 다양한 대기질 정보망이 구축될 것으로 기대한다.
Acknowledgments
이 논문은 2019년도 정부 (교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업입니다(NRF-2019R1I1A3A01062804). 본 연구에서 사용된 국내 도시대기측정망 자료를 제공해 주신 한국환경공단의 airkorea (https://www.airkorea.or.kr), 기상관측자료를 제공해 주신 기상자료개방포털 (https://data.kma.go.kr/), 인공위성 MODIS 자료를 제공해 주신 NASA의 Distributed Active Archive Center (https://ladsweb.modaps.eosdis.nasa.gov)와 국내 AERONET 관측 사이트 (Gangneung_WNU, Gwangju_GIST, Yonsei_University)를 구축, 유지 관리 및 자료 제공해주신 연구자분들께 감사드립니다.
References
-
Adar, S.-D., Filigrana, P.-A., Clements, N., Peel, J.-L. (2014) Ambient Coarse Particulate Matter and Human Health: A Systematic Review and Meta-Analysis, Current Environmental Health Reports, 8(1), 258-274.
[https://doi.org/10.1007/s40572-014-0022-z]

-
Atkinson, R.-W., Kang, S., Anderson, H.-R., Mills, I.-C., Walton, H.-A. (2014) Epidemiological Time Series Studies of PM2.5 and Daily Mortality and Hospital Admissions: a Systematic Review and Meta-Analysis, Thorax, 69, 660-665.
[https://doi.org/10.1136/thoraxjnl-2013-204492]

-
Bozdağ, A., Dokuz, Y., Gökçek, Ö.-B. (2020) Spatial Prediction of PM10 Concentration Using Machine Learning Algorithms in Ankara, Turkey, Environmental Pollution, 263, 114635.
[https://doi.org/10.1016/j.envpol.2020.114635]

-
Breiman, L. (2001) Random Forests, Machine Learning, 45(1), 5-32.
[https://doi.org/10.1023/A:1010933404324]

-
Charlson, R.-J., Schwartz, S.-E., Hales, J.-M., Cess, R.-D., Coakley Jr, J.-A., Hansen, J.-E., Hofmann, D.-J. (1992) Climate Forcing by Anthropogenic Aerosols, Science, 255(5043), 423-430.
[https://doi.org/10.1126/science.255.5043.423]

-
Cho, H.-Y., Kim, Y.-H., Im, H.-H. (2018) Forecast of Wind-Shear Alert Using Deep Neural Networks, Asia-pacific Journal of Multimedia Services Convergent with Art, Humanities, and Sociology, 8(7), 749-757.
[https://doi.org/10.21742/AJMAHS.2018.07.25]

-
Cho, K.-H., Lee, B.-Y., Kwon, H.-M., Kim, S.-C. (2019) Air Quality Prediction Using a Deep Neural Network Model, Journal of Korean Society for Atmospheric Environment, 35(2), 214-225, (in Korean with English abstract).
[https://doi.org/10.5572/KOSAE.2019.35.2.214]

- Choi, S.-I., Ahn, J., Cho, Y.-M. (2018) Review of Analysis Principle of Fine Dust, Korean Industrial Chemistry, 21(2), 16-23.
-
Cortes, C., Vapnik, V. (1995) Support-Vector Networks, Machine Learning, 20, 273-297.
[https://doi.org/10.1007/BF00994018]

-
Czernecki, B., Marosz, M., Jędruszkiewicz, J. (2021) Assessment of Machine Learning Algorithms in Short-term Forecasting of PM10 and PM2.5 Concentrations in Selected Polish Agglomerations, Aerosol and Air Quality Research, 21(7), 200586.
[https://doi.org/10.4209/aaqr.200586]

-
Giles, D.-M., Sinyuk, A., Sorokin, M.-G., Schafer, J.-S., Smirnov, A., Slutsker, I., Eck, T.-F., Holben, B.-N., Lewis, J.-R., Campbell, J.-R., Welton, E.-J., Korkin, S.-V., Lyapustin, A.-I. (2019) Advancements in the Aerosol Robotic Network (AERONET) Version 3 Database-automated Near-real-time Quality Control Algorithm with Improved Cloud Screening for Sun Photometer Aerosol Optical Depth (AOD) Measurements, Atmospheric Measurement Techniques, 12(1), 169-209.
[https://doi.org/10.5194/amt-12-169-2019]

-
Intergovernmental Panel on Climate Change (IPCC) (2022) Climate Change 2022: Mitigation of Climate Change.
[https://doi.org/10.1017/9781009157926]

-
Jeon, S.-H., Son, Y.-S. (2018) Prediction of Fine Dust PM10 Using a Deep Neural Network Model, The Korean Journal of Applied Statistics, 31(2), 265-285, (in Korean with English abstract).
[https://doi.org/10.5351/KJAS.2018.31.2.265]

- Kasten, F., Young, A.-T. (1989) Revised Optical Air Mass Tables and Approximation Formula, Applied Optics, 28(22), 4735-4738.
-
Kaufman, Y.-J., Tanré, D., Remer, L.-A., Vermote, E.-F., Chu, A., Holben, B.-N. (1997a) Operational Remote Sensing of Tropospheric Aerosol over Land from EOS Moderate Resolution Imaging Spectroradiometer, Journal of Geophysical Research: Atmospheres, 102(D14), 17051-17067.
[https://doi.org/10.1029/96JD03988]

-
Kaufman, Y.-J., Wald, A.-E., Remer, L.-A., Gao, B.-C., Li, R.-R., Flynn, L. (1997b) The MODIS 2.1-μm Channel-Correlation with Visible Reflectance for Use in Remote Sensing of Aerosol, IEEE transactions on Geoscience and Remote Sensing, 35(5), 1286-1298.
[https://doi.org/10.1109/36.628795]

-
Kim, B.-Y., Lim, Y.-K., Cha, J.-W. (2022b) Short-term Prediction of Particulate Matter (PM10 and PM2.5) in Seoul, South Korea Using Tree-based Machine Learning Algorithms, Atmospheric Pollution Research, 13(10), 101547.
[https://doi.org/10.1016/j.apr.2022.101547]

-
Kim, D.-H., Hwang, K.-Y., Yoon, Y. (2019) Prediction of Traffic Congestion in Seoul by Deep Neural Network, The Journal of the Korea Institute of Intelligent Transport Systems, 18(4), 44-57, (in Korean with English abstract).
[https://doi.org/10.12815/kits.2019.18.4.44]

-
Kim, Y.-I., Lee, K.-H., Lee, K.-T. (2022a) Evaluation and Prediction of Column Aerosol by Using the Time Series Machine Learning Technique, Journal of Korean Society for Atmospheric Environment, 38(1), 57-73, (in Korean with English abstract).
[https://doi.org/10.5572/KOSAE.2022.38.1.57]

-
Kim, Y.-I., Lee, K.-H., Park, S.-H. (2023) Application and Evaluation of Machine Learning Techniques for Real-time Short-term Prediction of Air Pollutants, Journal of Korean Society for Atmospheric Environment, 39(1), 107-127, (in Korean with English abstract).
[https://doi.org/10.5572/KOSAE.2023.38.1.107]

- Korean Institute of Environmental Science and Technology (KIEST) (2007) A Development of Air Quality Forecasting System.
-
Kujawska, J., Kulisz, M., Oleszczuk, P., Cel, W. (2022) Machine Learning Methods to Forecast the Concentration of PM10 in Lublin, Poland, Energies, 15(17), 6428.
[https://doi.org/10.3390/en15176428]

-
Lee, K.-H., Bae, M.-S. (2021) Discrepancy Between Scientific Measurement and Public Anxiety about Particulate Matter Concentrations, Science of The Total Environment, 760, 143980.
[https://doi.org/10.1016/j.scitotenv.2020.143980]

-
Lee, K.-H., Kim, Y.-J. (2010) Satellite Remote Sensing of Asian Aerosols: A Case Study of Clean, Polluted, and Asian Dust Storm Days, Atmospheric Measurement Techniques, Copernicus GmbH, 3, 1771-1784.
[https://doi.org/10.5194/amt-3-1771-2010]

-
Lee, K.-H., Shin, S.-K. (2022) Effect of Reduced Emissions from Thermal Power Plants in China on Local Air Quality Improvement, Journal of Korean Society for Atmospheric Environment, 38(2), 304-317, (in Korean with English abstract).
[https://doi.org/10.5572/KOSAE.2022.38.2.304]

-
Lee, K.-H., Wong, M.-S., Kim, K., Park, S.-S. (2014) Analytical Approach to Estimating Aerosol Extinction and Visibility from Satellite Observations, Atmospheric Environment, 91, 127-136.
[https://doi.org/10.1016/j.atmosenv.2014.03.050]

-
Lee, K.-H., Wong, M.-S., Li, J. (2022) Review of Atmospheric Environmental Change from Earth Observing Satellites, Asian Journal of Atmospheric Environment, 16(1), 1-13.
[https://doi.org/10.5572/ajae.2021.147]

-
Li, J., Wong, M.-S., Lee, K.-H., Nichol, J., Chan, P.-W. (2021) Review of Dust Storm Detection Algorithms for Multispectral Satellite Sensors, Atmospheric Research, 250, 105398.
[https://doi.org/10.1016/j.atmosres.2020.105398]

-
Michalsky, J.-J. (1988) The Astronomical Almanac’s Algorithm for Approximate Solar Position (1950-2050), Solar Energy, 40(3), 227-235.
[https://doi.org/10.1016/0038-092X(88)90045-X]

- National Institute of Environmental Research (NIER) (2021) Air Environment Annual Report.
-
Park, S.-H., Kim, M.-A., Im, J.-H. (2021) Estimation of Ground-level PM10 and PM2.5 Concentrations Using Boosting-based Machine Learning from Satellite and Numerical Weather Prediction Data, Korean Journal of Remote Sensing, 37(2), 321-335, (in Korean with English abstract).
[https://doi.org/10.7780/kjrs.2021.37.2.11]

-
Son, S.-H., Kim, J.-S. (2020) Evaluation and Predicting PM10 Concentration Using Multiple Linear Regression and Machine Learning, Korean Journal of Remote Sensing, 36(6-3), 1711-1720, (in Korean with English abstract).
[https://doi.org/10.7780/kjrs.2020.36.6.3.7]

-
Song, Z., Chen, B., Huang, Y., Dong, L., Yang, T. (2021) Estimation of PM2.5 Concentration in China Using Linear Hybrid Machine Learning Model, Atmospheric Measurement Techniques, 14(8), 5333-5347.
[https://doi.org/10.5194/amt-2021-64]

-
Suleiman, A., Tight, M.-R., Quinn, A.-D. (2019) Applying Machine Learning Methods in Managing Urban Concentrations of Traffic-related Particulate Matter (PM10 and PM2.5), Atmospheric Pollution Research, 10(1), 134-144.
[https://doi.org/10.1016/j.apr.2018.07.001]

-
Tanré, D., Kaufman, Y.-J., Herman, M., Mattoo, S. (1997) Remote Sensing of Aerosol Properties over Oceans Using the MODIS/EOS Spectral Radiances, Journal of Geophysical Research: Atmospheres, 102(D14), 16971-16988.
[https://doi.org/10.1029/96JD03437]

-
Wei, X., Chang, N.-B., Bai, K., Gao, W. (2020) Satellite Remote Sensing of Aerosol Optical Depth: Advances, Challenges, and Perspective, Critical Reviews in Environmental Science and Technology, 50(16), 1640-1725.
[https://doi.org/10.1080/10643389.2019.1665944]

-
Yang, G., Lee, H.-M., Lee, G.-Y. (2020) A Hybrid Deep Learning Model to Forecast Particulate Matter Concentration Levels in Seoul, South Korea, Atmosphere, 11(4), 348.
[https://doi.org/10.3390/atmos11040348]

김영일 (강릉원주대학교 공간정보협동과정 석사과정) (kyi3619@gmail.com)
이권호 (강릉원주대학교 대기환경과학과 교수) (kwonho.lee@gmail.com)