대기오염물질의 실시간 단기 예측을 위한 머신러닝 기법의 적용 및 평가

1. 서 론

대기오염은 여러 환경오염 중에서 피해규모가 가장 크게 나타나며, 환경오염으로 인한 질병발생 측면에서도 큰 비중을 차지하고 있다. WHO (2014)에서는 대기오염으로 인해 약 700만 명의 인구가 조기 사망한 것으로 추정하였고, 지난 조사 대비 사망자수가 2배 이상 증가하였으며, 이는 총 사망의 12.5%에 달한다고 보고하였다. 동아시아가 포함한 서태평양 지역에서도 대기오염으로 인한 사망이 약 200만 명으로 보고되어 국내에서도 대기질에 대한 연구와 지속적인 관리가 요구되고 있다 (Shin, 2007).

국내에서는 1989년부터 현재까지 지속적으로 국내 대기오염물질을 모니터링하고 있으며, 대기오염 기준물질 중 SO₂, CO, PM₁₀, PM_2.5 농도는 최근까지 꾸준히 감소 추세에 있고, NO₂와 O₃의 경우는 다른 오염물질과는 다르게 계속 증가하고 있는 것으로 알려져 있다 (NIER, 2021). 대기오염물질은 발생원과 이동과정에 대한 정확한 정보를 획득하기 어려우므로 일반적으로 사용되고 있는 수리물리적 수치 모델과 화학 반응식이 결합된 화학수송 모델을 이용한 방법 (Choi et al., 2019; Oh et al., 2016; KIEST, 2007), 그리고 통계적 모델을 이용한 대기질 예측에 관한 연구가 꾸준히 진행되어 왔다 (Goyal et al., 2006; Hooyberghs et al., 2005). 이 중 통계적 모델은 수치 모델에 비해서 연산속도가 매우 빠르다는 장점이 있으며, 자료의 구성과 통계적 계산과정이 적절하게 구현된 통계적 모델의 예측 정확도 또한 수치 모델보다 높은 것으로 보고되어 있다 (Hrust et al., 2009).

최근에는 수리적 통계기법으로서 머신러닝 및 딥러닝 기법을 이용하여 대기오염물질의 농도를 예측하는 시도가 국내외적으로 많이 진행되고 있다. 예를 들면, Pyo et al. (2021) 연구에서는 서울과 강릉의 컬럼에어로솔 자료와 기상 자료를 이용하여 K-means 클러스터링에 적용하여 비교한 결과, 서울과 강릉 각각 6개, 4개의 시나리오로 분류되었으며 서울은 남풍이 불 때 Aerosol Optical Depth (AOD)가 가장 높고, 강릉은 남서풍이 불 때 AOD가 가장 높은 것으로 보고하였다. Cho et al. (2019) 연구에서는 Deep Neural Network (DNN) 기법을 이용하여 전국 광역시 도시대기측정망의 대기오염물질 농도를 예측한 결과, CO와 SO₂의 경우 관측등급 일치도가 90% 이상이었으며, PM₁₀, PM_2.5에 대한 예측 결과는 약 60~70%로 비교적 정확도가 낮았음을 보였다. 또한 대기 중 입자상 물질의 총 부하량을 나타내는 컬럼에어로솔을 시계열 머신러닝에 적용하여 학습시간에 따라 예측한 결과, 학습기간이 1년일 때 평균 제곱근 오차 (Root Mean Squared Error, RMSE)가 0.285, bias가 0.202로 가장 정확도가 높아 시계열 머신러닝을 이용한 컬럼에어로솔 예측은 단기예측이 우수한 것으로 보고된 연구도 진행되었다 (Kim et al., 2022).

비교적 최근에는 Kim and Jeong (2022)의 연구에서 DNN, Random Forest (RF), Support Vector Regression (SVR), Long Short Term Memory (LSTM) 4가지 기법을 사용하여 서울 지역의 미세먼지 농도를 예측한 결과, 등급별 정확도는 84~88%로 모델 간 예측 정확도의 차이가 있었으며 SVR 모델의 정확도가 가장 높게 나타난 것으로 보고되었다. 또한, 컬럼에어로솔 자료를 기반으로 은닉층에 따른 DNN 기법의 에어로솔에 의한 복사강제력의 정확도를 비교한 결과, 특정 에어로솔 타입이 은닉층의 구조가 5-4-3-2 구조로 훈련시켰을 때 R=0.97, Bias=0.68, RMSE=6.51로 정확도가 높고, 기존 복사전달모델을 이용할 때보다 DNN 모델을 구축하여 에어로솔에 의한 복사강제력을 산출할 때 소요시간이 월등히 빠르다는 연구가 진행되었다 (Pyo and Lee, 2022). 국외에서는 미국 캘리포니아 지역의 U.S. Environmental Protection Agency (US EPA) 대기질 자료를 입력자료로 Support Vector Machine (SVM) 기법에 적용하여 CO, NO₂, SO₂, O₃, PM_2.5 농도를 예측한 결과, SO₂의 경우 결정계수 (R²)가 0.023으로 가장 정확도가 낮았고 O₃은 R² 값이 0.923으로 가장 높은 수준의 정확도가 나타났다 (Castelli et al., 2020). 현재까지, 개별적인 머신러닝 기법을 이용하여 특정 지역의 대기질을 예측하거나 제한된 방법론을 이용하여 예측하는 사례가 보고되고 있으나, 다양한 머신러닝 기법을 이용한 결과를 비교 평가하여 대기오염물질을 예측할 수 있는 최적화된 모델을 구축한 연구 사례는 드문 실정이다.

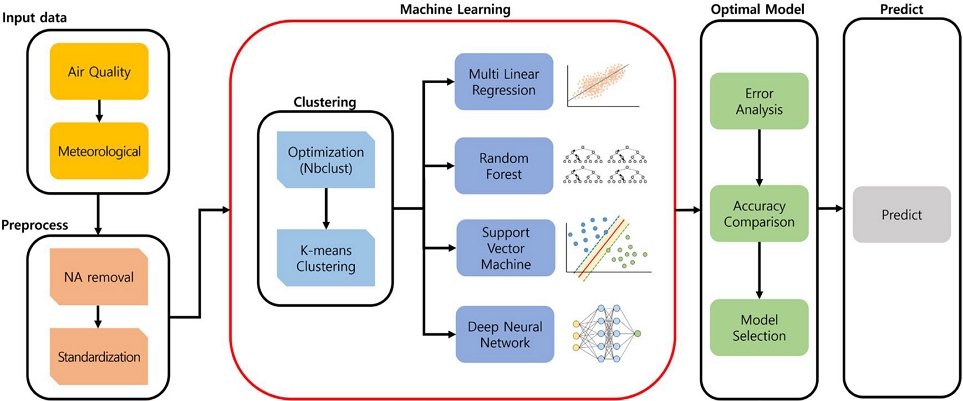
따라서, 본 연구는 대기질 및 기상 자료를 기반으로 주요 머신러닝 기법 (RF, SVM, Multiple Linear Regression (MLR), DNN)을 훈련시킨 결과에 대한 정확도 평가를 기반으로 최적의 대기질 예측 모델을 선정하였다. 이를 위해, 첫째, 국내의 지역별 대기질 변화 특성이 고려된 머신러닝 학습시스템을 구축하기 위하여 ML 클러스터링 기반의 지역별 대기질 특성을 분류하였다. 둘째, 앞에서 언급된 네 가지 머신러닝 기법을 독립적으로 학습한 결과를 비교 및 평가하여 최적의 대기질 예측 모델을 선정하였다. 마지막으로, 선정된 대기질 예측 모델을 이용하여 실제 대기오염물질의 단기 예측 및 고농도 사례에 대한 적용을 통하여 선정된 최적의 ML 기반의 대기질 예측 모델에 대한 성능을 검증하였다.

2. 자료 및 방법

2. 1 관측 자료

연구 대상 지역은 대한민국에 위치한 주요 인구 밀집 지역 6개의 관측 지점인 광주광역시 (35.155°N, 126.889°E agl.), 대구광역시 (35.865°N, 128.640°E agl.), 대전광 역시 (36.372°N, 127.374°E agl.), 부산광역시 (35.100°N, 129.030°E agl.), 서울특별시 (37.572°N, 127.005°E agl.), 울산광역시 (35.560°N, 129.371°E agl.)와 지형적 특성이 비교적 뚜렷하게 나타나는 강릉시 (37.760°N, 128.903°E agl.), 목포시 (34.806°N, 126.372°E agl.), 원주시 (37.353°N, 127.947°E agl.), 제주시 (33.500°N, 126.531°E agl.) 4개의 관측 지점을 포함한다 (그림 1).

Fig. 1.

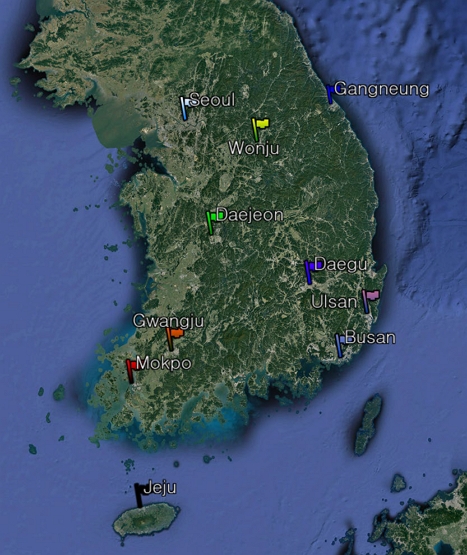
Geographic locations of six Sun-sky radiometer measurement sites used in this study (Busan (35.100°N, 129.030°E agl.), Daegu (35.865°N, 128.640°E agl.), Daejeon (36.372°N, 127.374°E agl.), Gangneung (37.760°N, 128.903°E agl.), Gwangju (35.155°N, 126.889°E agl.), Jeju (33.500°N, 126.531°E agl.), Mokpo (34.806°N, 126.372°E agl.), Seoul (37.572°N, 127.005°E agl.), Ulsan (35.560°N, 129.371°E agl.), and Wonju (37.353°N, 127.947°E agl.)).

본 연구에서 사용된 머신러닝 기법에 적용한 입력자료는 NO₂, CO, SO₂, O₃, PM₁₀, PM_2.5, 기온, 풍향, 풍속, 기압, 이슬점 온도, 시정, 상대습도 자료를 사용하였다. 도시대기측정망 자료는 Airkorea 데이터 베이스 (https://www.airkorea.or.kr)에서 수집하였고, Automated Synoptic Observing System (ASOS) 자료는 기상 자료개방포털 (https://data.kma.go.kr)에서 수집하였다. 관측 지점별 관측 기간과 자료에 대한 상세 설명은 표 1과 같다.

Table 1.

List of datasets used in this study.

2. 2 연구 방법

연구 대상 지역의 대기질 예측 모델 구축 및 평가를 위하여, 널리 사용되고 있는 머신러닝 기법 중 SVM, RF, MLR, DNN을 사용하여 입력값에 따른 개별 모델의 결과를 분석하였다. 그리고 각각의 모델 결과에 따른 오차 분석 과정을 통하여 최적의 예측 모델을 선정하였고, 실제 관측값과의 비교 평가를 통하여 모델 예측치에 대한 정확도 평가를 수행하였다. 본 연구에서 사용된 머신러닝 분석을 위한 자료처리는 오픈소스 통계패키지인 R을 이용하였다. R은 무료로 개방된 통계패키지로 모델링, 시계열 분석, 분류, 클러스터링 등 다양한 그래픽 기술을 제공한다는 장점이 있으며, 2023년 1월 13일 현재 통계 그래픽, 통계 계산 및 통계 모형과 관련 라이브러리가 19,028개가 존재하는 것으로 알려져 있다 (Jang, 2020).

2. 2. 1 머신러닝 클러스터링

각 연구 대상 지역의 대기질 변화 특성이 지역적으로 다르게 나타날 것으로 예상되므로, 머신러닝 클러스터링 기법을 적용하여 10개의 관측 지점에 대한 대기질 특성을 분류하였다. 머신러닝 클러스터링 기법 중 본 연구에서 사용된 K-Means 클러스터링 기법은 다차원의 데이터를 이용하여 클러스터의 중심을 수정하며 군집을 반복적으로 분류하는 일종의 분할 클러스터링 알고리즘이다 (Ahmad and Dey, 2007). 본 연구에서는 NO₂, CO, SO₂, O₃, PM₁₀, PM_2.5, 기온, 풍향, 풍속, 기압, 이슬점 온도, 시정, 상대습도 자료에 대한 지역별 분류 모델의 입력자료로 사용하였다. 머신러닝 클러스터링 수행에 앞서 각 입력자료에 대해 시공간 일치, 결측값 제거, 데이터 표준화 작업을 수행하였고, 최적의 클러스터 수를 지정하기 위해 Nbclust 패키지 (Charrad et al., 2014)를 이용하였다.

2. 2. 2 Random Forest

머신러닝 기법 중 널리 사용되고 있는 RF 기법은 앙상블 기법을 이용하는 여러 개의 의사결정 나무 (Decision Tree, DT)를 기반으로 한 머신러닝 기법이다 (Breiman, 2021). 즉, 입력자료에 대한 해석력이 좋지만 상대적으로 모델링 예측력이 떨어지고 데이터에 따른 결과값의 불안정성을 가지는 DT 기법을 보완하기 위해 개발된 기법이다. RF 기법은 학습과정에서 구성된 여러 개의 의사결정 나무로 인해 회귀 또는 분류를 하는 알고리즘이며 각 가지에서 최적 분리점과 최적 분리 변수를 결정하고 다수결의 원칙을 이용하여 예측값을 결정한다 (Choi and Seo, 1999). RF 기법은 해석이 어렵다는 단점이 있지만, 데이터 용량이 방대해도 속도가 빠르고 비선형성을 가진 변수 간의 관계를 잘 반영하고 예측력이 매우 높다는 장점이 있다. 본 연구에서는 R의 Caret 및 RF 패키지를 이용하여 RF 모델을 구축하였다.

2. 2. 3 Support Vector Machine

SVM 기법은 Cortes and Vapnik (1995)에 의해 제안된 머신러닝 기법으로, 비선형 문제를 특정 고차원 공간의 선형 문제로 나타내기 때문에 수학적으로 분석하기에 수월하다 (Hearst et al., 1998). 또한 설정해야 하는 파라미터 수가 많지 않아 비교적 간단하게 학습할 수 있으며, 구조적 위험을 최소화하여 과적합을 방지한다. SVM 기법은 자료 분석, 패턴 인식 등을 위한 머신러닝 기법으로 정확도가 높은 것으로 보고되고 있으며, 선형 데이터와 비선형 데이터에 대한 분석이 가능하다는 장점이 있다. 본 연구에서는 R의 e1071 패키지를 이용하여 SVM 모델을 구축하였다.

2. 2. 4 Multiple Linear Regression

MLR 기법은 종속변수와 독립변수 간의 관계를 나타내는 선형 회귀 중에서 여러 개의 독립변수와 종속변수 간의 관계를 나타내는 기법으로, 식 (1)과 같은 내부 방정식이 사용된다.

$\[ Y={\sum }_{i=0}^n{A}_i{X}_i+\epsilon \]$

(1)

식 (1)에서 Y는 종속변수, n은 독립변수의 개수, i는 다중회귀식의 차수, A_i는 회귀계수, X_i는 독립변수, ε는 확률 오차를 의미한다. 본 연구에서는 MLR 모델을 구축하기 위해 R에서 제공되는 기본 선형회귀모델을 이용하였으며, 종속변수는 예측하고자 하는 대기오염물질, 독립변수는 그 외 대기오염물질과 기상 자료로 지정하여 MLR 모델을 구축하였다.

2. 2. 5 Deep Neural Network

인공신경망 기법은 인간 두뇌의 뉴런을 모방하여 입력층, 은닉층, 출력층으로 구성되며, 입력자료는 신경망 내부에서 정의된 복잡한 가중치 계산과 활성화 함수를 이용하여 최종 결과를 얻는 기법이다 (Lee et al., 2012). LeCun et al. (1989)에 의해 제안된 DNN은 인공신경망의 구조에서 은닉층이 여러 개 존재하는 기법이다. DNN 기법에 처음 제안될 당시 학습에 소요되는 시간이 오래 걸린다는 단점이 존재하여 크게 각광받지는 못했지만 (Kim et al., 2019), 최근의 컴퓨터 하드웨어의 발전으로 널리 사용되는 인공지능 기법이다. DNN 기법은 비선형성을 가진 데이터에 대해 학습이 가능하고 예측 정확도가 높은 것으로 보고되었다. 본 연구에서는 경사하강법을 이용하여 오차를 줄이는 역전파 알고리즘을 적용하였으며, R의 Neuralnet 패키지를 이용하여 DNN 모델을 구축하였다 (Günther and Fritsch, 2010).

2. 2. 6 대기질 단기 예측 모델

본 연구에서는 대기질 단기 예측 모델의 출력변수는 국내 대기오염관측망에서 측정되고 있는 대기오염 기준물질 (NO₂, CO, SO₂, O₃, PM₁₀, PM_2.5) 중 한 가지 종류의 오염물질이며, 모델의 입력변수는 표 1에서 언급된 기상 자료 (기온, 풍향, 풍속, 기압, 이슬점 온도, 시정, 상대습도)와 출력자료에서 사용되지 않은 나머지 다섯 가지의 대기오염물질이다. 모델 구축을 위하여 기상 자료와 대기질 관측 자료는 동일한 관측시간 자료만 사용하였으며, 각 관측단위는 평균값과 표준편차를 이용하여 표준화된 자료를 사용하였다. 표준화된 입력자료는 머신러닝 모델의 학습 (Training), 시험 (Test), 검증 (Validation)을 위한 부분으로 각각 분리하였으며, Training set와 Test set는 2015년 1월 1일부터 2018년 12월 31일까지의 관측 자료 중 무작위로 8 : 2=Training : Test의 비율로 구분하여 모델의 성능을 분석하였다. 검증 단계에서는 2019년 1년 동안의 기간을 선정하여 대기질 예측 모델과 실제 관측 결과를 비교하여 모델의 정확도를 검증하였다.

대기질 예측 모델의 성능 평가 및 정확도를 비교하기 위한 지수값으로서, 평균 절대 오차 (Mean Absolute Error, MAE), 평균 제곱근 오차 (Root Mean Squared Error, RMSE), 평균 절대비 오차 (Mean Absolute Percentage Error, MAPE)와 R²를 계산하였다. MAE, RMSE, MAPE, R²는 관측값과 모델 예측값의 회귀 및 상관 지표를 다룰 때 사용되며, 모델의 정확도를 확인할 때 사용된다. MAE는 식 (2)와 같이 모델 예측값 ($$ {\overline{y}}_i$$)과 관측값(y_i)의 차이에 대한 절대값을 평균한 값이며, 예측값의 오차가 선형적으로 반영되므로 이상치가 많은 경우 값이 커진다.

$\[ \mathrm{M}\mathrm{A}\mathrm{E}=\frac{1}{n}{\sum }_{i=1}^n\left|y_i-{\overline{y}}_i\right| \]$

(2)

위 식에서 n은 총 데이터의 개수이며, i는 모델 입력값에 따른 순서이다. RMSE는 식 (3)과 같이 오차에 대한 제곱값을 평균하기 때문에 오차가 크면 클수록 기하급수적으로 증가하는 결과를 나타내므로 MAE보다는 오차의 크기에 민감하게 반응한다.

$\[ \mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{\frac{1}{n}{\sum }_{i=1}^n{\left(y_i-{\overline{y}}_i\right)}^2} \]$

(3)

MAPE는 식 (4)와 같이 상대오차의 절대값을 100분율로 변환한 것으로, 관측값 대비 모델 예측오차에 대한 편향이 존재한다.

$\[ \mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}=100\times \frac{1}{n}{\sum }_{i=1}^n\left|\frac{y_i-{\overline{y}}_i}{y_i}\right| \]$

(4)

R²는 식 (5)와 같이 계산되며, 두 값에 대한 회귀분석모델이 얼마나 데이터를 잘 설명해주는지를 나타내는 값으로서, 0~1 사이에서 1에 가까울수록 설명이 높은 것을 의미한다.

$\[ R^2=1-\frac{{\sum }_{i=1}^n{\left({\overline{y}}_i-{\acute{y}}_i\right)}^2}{{\sum }_{i=1}^n{\left(y_i-{\acute{y}}_i\right)}^2} \]$

(5)

위 식에서, $$ {\acute{y}}_i$$는 도시대기측정망 관측값의 평균값이다. MAE, RMSE, MAPE는 값이 작을수록 정확도가 높은 것을 의미하고 값이 클수록 정확도가 다소 떨어지는 것을 의미한다. 반대로, R²의 경우 값이 클수록 정확도가 높으며, 값이 작을수록 정확도가 낮은 것을 의미한다.

본 연구에서는 각 관측 지점에 대한 최적의 대기질 예측 모델을 결정하기 위하여 각각의 머신러닝 기법에 대한 훈련 결과에 대한 정확도를 평가한 후, 최적의 모델을 이용하여 대기질 예측을 수행하였다. 최적의 대기질 예측 모델을 결정하기 위한 과정에서는 실제 관측한 대기질 농도값과 예측 모델을 통해 산출된 예측값을 비교하여 대기질 예측 모델의 정확도를 비교하여 최적의 대기질 예측 모델을 선정하였다. 결정된 최적의 대기질 예측 모델은 이후, 실제 사례에 적용하여 대기질 예측 모델의 성능을 평가하였다. 본 연구의 자료처리흐름도는 그림 2와 같다.

Fig. 2.

Flowchart of data processing used in this study.

3. 결과 및 토의

3. 1 지역 군집 선정

그림 1에서 제시된 국내 10개 지점의 대기질 특성을 지역별로 분류하기 위해 기온, 풍향, 풍속, 기압, 이슬점 온도, 시정, 상대습도, NO₂, CO, SO₂, O₃, PM₁₀, PM_2.5를 입력자료로 사용하는 머신러닝 클러스터링 기법에 적용하였다. 클러스터링 분류를 위하여 먼저 데이터의 클러스터 개수를 정해야 하며, 최적의 클러스터 개수의 선정을 위하여 30가지 클러스터링 테스트를 수행하였다. 그림 3의 결과와 같이 30가지의 결과 중 가장 많은 9개의 테스트 결과에서 3개의 클러스터로 분류하는 것이 분류 정확도가 가장 높은 것으로 나타났다. 따라서, 3개의 클러스터 개수로 한정하여 클러스터링 분석을 수행한 결과, Cluster 1은 서울 관측 지점, Cluster 2는 제주, 부산, 원주, 대전, 대구, 울산, 광주, 목포 관측 지점이며 Cluster 3은 강릉 관측 지점으로 분류되었다.

Fig. 3.

The optimal number of cluster in determined from the NbClust package (left) and K-means clustering results (right).

표 2는 각 클러스터별 대푯값을 나타내며, 각 클러스터별 기상관측값의 특징은 다음과 같다. Cluster 1은 상대적으로 온도가 낮고 (기온=8.08°C) 중간정도의 상대습도 (RH=66.31%)와 남풍계열의 바람이 약하게 부는 조건이다. Cluster 2의 대푯값은 기온이 21.71°C, 상대습도가 72.78%로 가장 높은 수치를 보였으며, 남풍계열의 바람과 다소 강하게 부는 조건을 나타냈다. Cluster 3의 경우는 기온이 7.29°C, 상대습도 47.44%로 가장 낮은 값을 나타냈으며. 서풍 계열의 주풍과 강한 풍속 (3.10 m/s)을 보였다. 대기오염물질의 경우, NO₂, CO, SO₂, PM₁₀, PM_2.5의 대푯값은 Cluster 1 (NO₂: 0.037 ppm, CO: 0.75 ppm, SO₂: 0.006 ppm, PM₁₀: 68.31 µg/m³, PM_2.5: 43.57 µg/m³)에서 가장 높은 농도를 보였으며 Cluster 2 (NO₂: 0.014 ppm, CO: 0.37 ppm, SO₂: 0.003 ppm, PM₁₀: 32.16 µg/m³, PM_2.5: 18.20 µg/m³)에서 가장 낮은 수준의 농도로 나타났다. 반면에 O₃의 대푯값은 Cluster 2에서 0.033으로 가장 높았으며 Cluster 1에서 0.015로 가장 낮았다. 그리고, 이러한 대푯값들로 분류되는 지역은 Cluster 1이 서울과 수도권의 고농도 대기질 특성을 대표하며, Cluster 3은 저농도 지역 (강릉), Cluster 2는 중간정도 수준의 대기질 특성을 나타내는 지역 (제주, 부산, 원주, 대전, 대구, 울산, 광주, 목포)으로 분류됨을 알 수 있었다.

Table 2.

Cluster analysis results using regional air quality data and meteorological data.

3. 2 대기질 예측 모델 선정

앞에서 언급된 머신러닝 기법 중 지역별 대기질 예측을 위하여 최적의 기법을 사용할 필요가 있다. 본 연구에서는 각 Cluster에 대하여 개별 머신러닝 기법을 적용하여 산출된 결과에 대한 상호 비교 분석 결과 중 비교적 정확도가 높은 기법을 최종적으로 선별하여 대기질 예측을 위하여 사용하였다. 각 대기오염물질에 대한 머신러닝 모델링을 수행하였으며, 대표적인 사례로서 PM₁₀, PM_2.5에 대한 최적 모델 결정과정을 설명하였다.

먼저, Cluster 1관측 자료를 기반으로 PM₁₀ 농도의 관측값과 예측값을 비교한 결과 중 가장 높은 정확도 (best)와 낮은 정확도 (worst)를 가지는 경우를 비교 한 결과는 그림 4(a), (b)와 같다. 그림 4(a)에서 사용된 DNN 기법의 결과, 각 검증지수는 MAE=5.43 µg/m³, RMSE=8.27 µg/m³, MAPE=15.91%, R²=0.94 로 Cluster 1 관측 자료의 PM₁₀ 예측 정확도가 가장 높게 나타났다. 반면에, 그림 4(b)는 MLR 기법을 적용했을 때 가장 낮은 정확도를 나타냈으며, MAE=6.93 µg/m³, RMSE=10.73 µg/m³, MAPE=20.85%, R²=0.89이었다. 그림 4(c), (d)에서 Cluster 2의 경우는 RF 기법을 적용한 결과가 가장 높은 정확도 (MAE=7.11 µg/m³, RMSE=10.35 µg/m³, MAPE=20.39%, R²=0.89)를 보였으며, MLR 기법에 적용하였을 때 가장 낮은 정확 도 (MAE=8.54 µg/m³, RMSE=12.16 µg/m³, MAPE=24.41%, R²=0.84)를 보였다. 그림 4(e), (f)는 Cluster 3의 관측 자료를 분석한 경우로서, RF 기법이 가장 높은 정확도 (MAE=6.80 µg/m³, RMSE=9.79 µg/m³, MAPE=18.23%, R²=0.89)를, MLR 기법이 가장 낮은 정확도 (MAE=8.92 µg/m³, RMSE=12.53 µg/m³, MAPE=24.57%, R²=0.81)를 보였다.

Fig. 4.

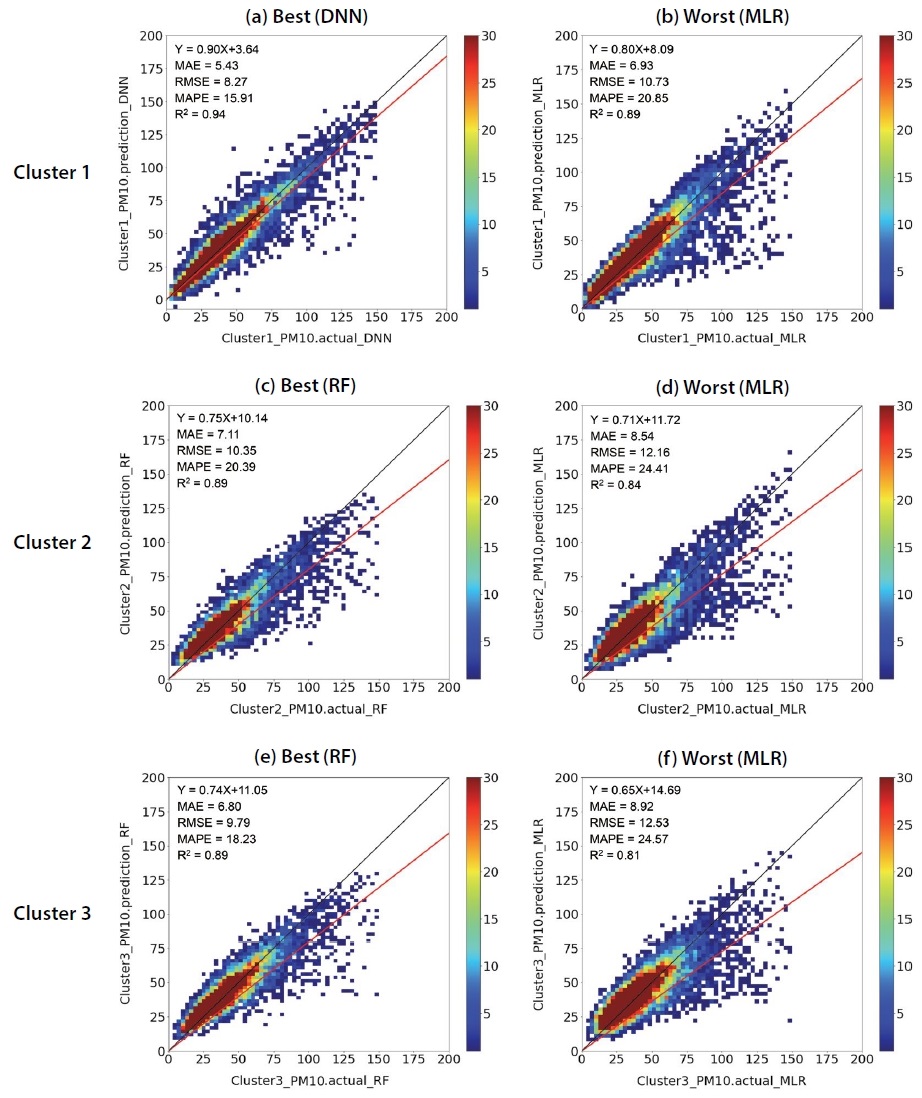
Scatterplots of model predicted and observed PM10 data for (a) Cluster 1 (best): DNN, (b) Cluster 1 (worst): MLR, (c) Cluster 2 (best): RF, (d) Cluster 2 (worst): MLR, (e) Cluster 3 (best): RF, (f) Cluster 3 (worst): MLR.

그림 5는 Cluster별 PM_2.5 농도에 대해 개별 머신러닝 기법에 적용한 결과 중 정확도가 가장 높은 경우와 가장 낮은 정확도의 사례를 비교한 결과를 나타낸다. 그림 5(a), (b)는 Cluster 1 관측 자료를 기반으로 PM_2.5 값의 실제 관측값과 예측값을 비교한 경우로서, RF 기법에 적용하였을 때 가장 높은 정확도 (MAE=3.34 µg/m³, RMSE=5.30 µg/m³, MAPE=20.27%, R²=0.9) 를 보였으며, MLR 기법의 적용 결과가 가장 낮은 정확도 (MAE=5.00 µg/m³, RMSE=7.40 µg/m³, MAPE=29.44%, R²=0.90)를 보였다. 그림 5(c), (d)는 Cluster 2 관측 자료에 대해 가장 높은 정확도는 RF 기법에 적용한 결과 (MAE=7.11 µg/m³, RMSE=10.35 µg/m³, MAPE=20.39%, R²=0.89)이며, 가장 낮은 정확도는 MLR 기법을 적용한 결과 (MAE=8.54 µg/m³, RMSE=12.16 µg/m³, MAPE=24.41%, R²=0.84)였다. 그림 5(e), (f)에서 Cluster 3 관측 자료는 RF 기법의 적용 결과 (MAE=4.07 µg/m³, RMSE=5.40 µg/m³, MAPE=28.48%, R²=0.90)와 MLR 기법의 적용 결과 (MAE=5.71 µg/m³, RMSE=7.55 µg/m³, MAPE=40.63%, R²=0.81) 각각 정확도가 가장 높은 것과 낮은 수준의 결과를 보였다.

Fig. 5.

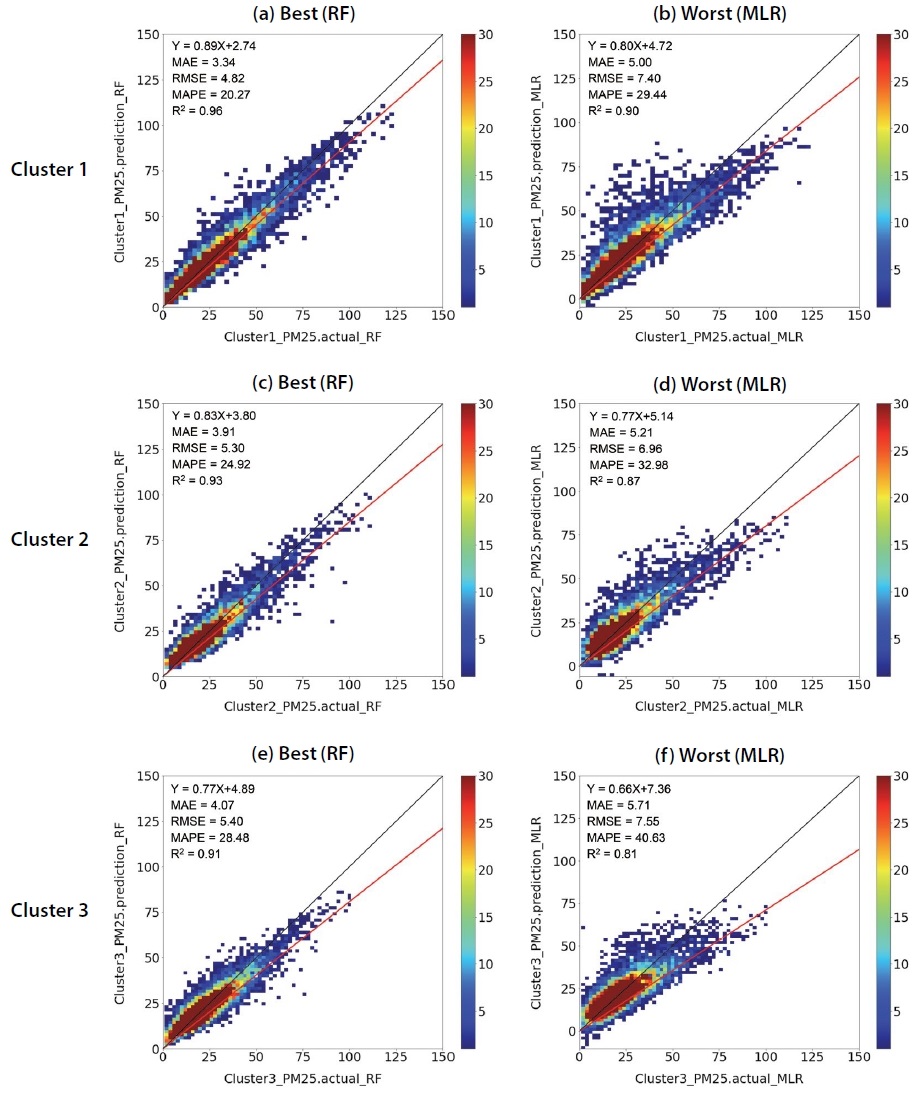
Scatterplots of model predicted and observed PM2.5 data for (a) Cluster 1 (best): RF, (b) Cluster 1 (worst): MLR, (c) Cluster 2 (best): RF, (d) Cluster 2 (worst): MLR, (e) Cluster 3 (best): RF, (f) Cluster 3 (worst): MLR.

이상의 결과를 종합하면, 각 지역 클러스터와 대기오염물질별로 머신러닝 기법의 적용 결과에 대한 정확도가 상이하게 나타나므로 단일 머신러닝 기법을 사용하기보다는 머신러닝 기법에 입력자료의 특성과 조건에 따라 최적의 모델을 적용해야 함을 증명하였다. 만일, 단일 머신러닝 기법이 전체 지역이나 모든 대기오염물질의 모델링에 사용된다면 모델링에 대한 계통 및 상대오차가 결과값이 미치는 영향이 상대적으로 크게 나타날 것으로 예상된다. 따라서, 본 연구에서는 다수의 머신러닝 기법 중 최적의 모델을 선정하여 대기오염물질에 대한 농도를 예측하고자 하였다.

이상의 개별 머신러닝 기법을 적용하여 산출된 학습 결과로부터 각 검증지수값에 대한등급을 A (3점), B (2점), C (1점), D (0점)와 같이 부과하여 총합 (Total Grade Number, TGN)이 가장 높은 모델을 최적의 예측 모델로 선정하였다. 표 3은 Cluster 1 관측 자료를 머신러닝 기법에 적용하여 나온 결과에 대한 검증지수값을 비교한 표이다. Cluster 1 관측 자료를 DNN와 RF 기법에 적용하여 PM₁₀ 농도를 예측하였을 때 TGN이 모두 9점으로 동일하였지만 DNN 기법에 적용할 때 A등급이 2번으로 더 많아 PM₁₀의 경우 DNN 모델을 최적의 모델로 선정하였다. NO₂, CO, SO₂, PM_2.5의 경우 RF (NO₂: 12, CO: 12, SO₂: 12, PM_2.5: 11) 모델에 적용한 결과가 가장 큰 TGN 값을 획득하였으므로 최적의 예측 모델로 선정하였다. O₃은 DNN 기법과 RF 기법에 적용할 때 TGN이 9점으로 동일하였지만 A등급이 RF 기법에 적용할 때 DNN 기법에 적용할 때보다 1개 더 많아 RF 모델을 최적의 예측 모델로 선정하였다. 반면에, MLR 기법에 적용하여 예측한 결과 6가지 대기오염물질 모두 TGN이 0점으로 정확도가 가장 낮았다.

Table 3.

MAE, RMSE, MAPE, R2 for different machine learning methods and total grade number (TGN) of Cluster 1.

Cluster 2 관측 자료를 머신러닝 기법에 적용한 결 과에 대한 검증지수값을 비교한 결과는 표 4와 같다. Cluster 2 관측 지점에서는 6가지 대기오염물질 모두 RF 기법에 적용하여 예측할 때, TGN이 제일 높아 RF (NO₂: 11, CO: 12, SO₂: 11, O₃: 10, PM₁₀: 11, PM_2.5: 12) 모델이 최적의 예측 모델로 선정하였다. Cluster 1과 마찬가지로 Cluster 2 또한 MLR 기법을 적용한 경우에서 제일 낮은 TGN 값을 보였다.

Table 4.

MAE, RMSE, MAPE, R2 for different machine learning methods and total grade number (TGN) of Cluster 2.

표 5는 Cluster 3 관측 자료를 4가지 머신러닝 기법에 적용한 결과에 대한 검증지수값을 비교한 표이다. NO₂의 경우 DNN 기법을 이용하여 예측 모델을 구축할 때 TGN이 12로 가장 정확도가 높았으며, 나머지 대기오염물질인 CO, SO₂, O₃, PM₁₀, PM_2.5은 RF (CO: 12, SO₂: 12, O₃: 10, PM₁₀: 11, PM_2.5: 11) 기법에 적용하였을 때 TGN이 가장 높아 최적의 예측 모델로 선정하였다. 앞서 두 Cluster와 마찬가지로 Cluster 3도 MLR 모델을 적용하여 예측 모델을 구축하였을 때 TGN이 제일 낮아 예측 정확도가 가장 낮았다.

Table 5.

MAE, RMSE, MAPE, R2 for different machine learning methods and total grade number (TGN) of Cluster 3.

3. 3 대기질 예측 모델 적용 결과

앞서 선정된 최적의 대기질 예측 모델을 이용하여 2019년 1월 1일부터 2019년 12월 31일까지의 기간을 선정하여 모델의 예측 결과와 실제 관측값과의 비교검증을 수행하였으며, 해당 기간 동안에 대한 모델 예측 정확도 검증수치를 각각 계산하였다.

먼저 Cluster 1에 대한 사례 비교 결과는 그림 6과 같으며, SO₂를 제외한 NO₂, CO, O₃, PM₁₀, PM_2.5의 모델링 예측값과 관측값은 모두 0.9 이상의 높은 R² 값을 보였다. SO₂는 두 값의 상관관계는 상대적으로 낮지만, 다른 대기오염물질 대비 매우 낮은 관측값의 범위이므로 오차범위도 MAE=0.0006 ppm, RMSE=0.0007 ppm으로서 모델의 예측 정밀도는 비교적 높은 것으로 평가할 수 있다. 기체상 물질인 NO₂, CO, SO₂, O₃의 상대오차율 MAPE는 각각 18.68%, 13.34%, 15.83%, 41.50%로서 O₃의 경우가 상대적으로 큰 값을 보였다. PM₁₀, PM_2.5의 상대오차율 MAPE는 각각 14.75%, 16.51%로서 낮은 수치를 보였다.

Fig. 6.

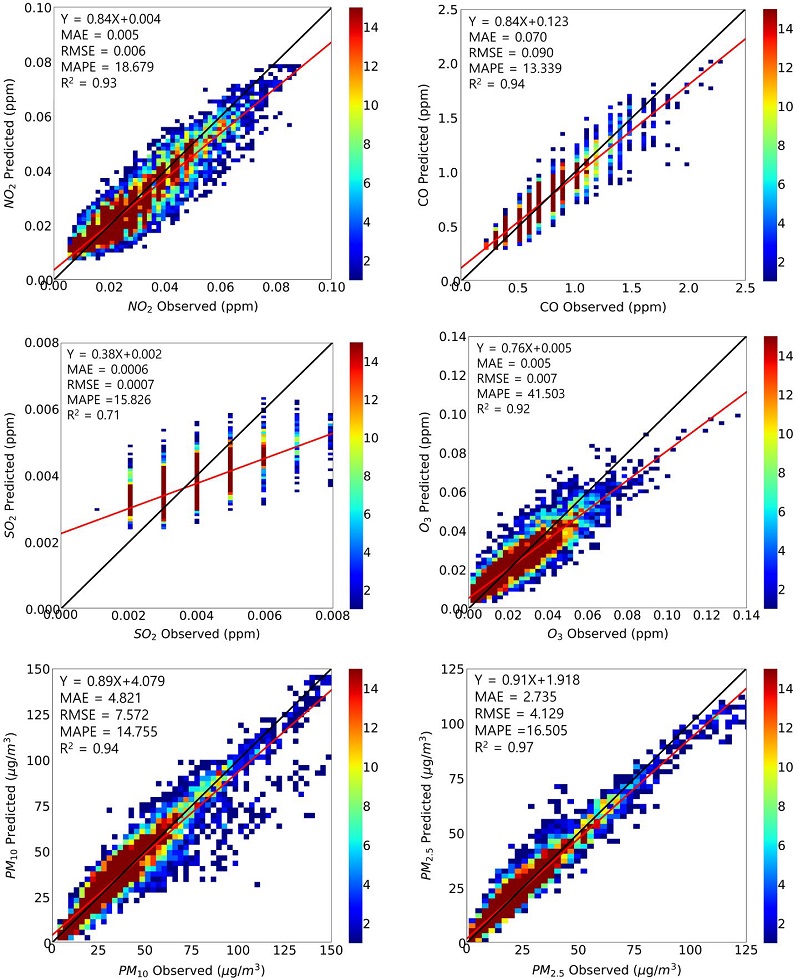
Scatterplots of optimal model prediction and observed air pollutants concentrations for Cluster 1 during a year of 2019.

그림 7은 Cluster 2에 대한 사례 비교 결과로서, Cluster 1의 결과와 마찬가지로 SO₂를 제외한 NO₂, CO, O₃, PM₁₀, PM_2.5의 모델링 예측값과 관측값이 모두 0.85 이상의 높은 R² 값을 보였다. NO₂, CO, SO₂, O₃, PM₁₀, PM_2.5의 MAE=0.003 ppm, 0.06 ppm, 0.0006 ppm, 0.006 ppm, 4.853 µg/m³, 3.165 µg/m³, RMSE=0.004 ppm, 0.079 ppm, 0.0008 ppm, 0.008 ppm, 7.106 µg/m³, 4.356 µg/m³으로서 평균 오차범위가 상대적으로 낮은 범위에 있었으며, 상대오차율 MAPE는 각각 20.07%, 20.18%, 28.76%, 16.92%, 14.20%, 23.52%였다. Cluster 1과 비교하여 Cluster 2에 대한 O₃의 예측 결과가 상대적으로 더욱 높게 나타났는데, 이는 오존의 관측 농도 범위가 상대적으로 더욱 크기 때문인 것으로 보인다.

Fig. 7.

Scatterplots of optimal model prediction and observed air pollutants concentrations for Cluster 2 during a year of 2019.

Cluster 3에 대한 사례 비교 결과는 그림 8과 같으며 Cluster 1, 2와는 다르게 SO₂, CO를 제외한 NO₂, O₃, PM₁₀, PM_2.5의 모델링 예측값과 관측값이 모두 0.8이상의 높은 R² 값을 보였다. NO₂, CO, SO₂, O₃, PM₁₀, PM_2.5의 MAE=0.004 ppm, 0.077 ppm, 0.0007 ppm, 0.006 ppm, 6.502 µg/m³, 3.874 µg/m³, RMSE=0.004 ppm, 0.090 ppm, 0.001 ppm, 0.008 ppm, 9.632 µg/m³, 5.360 µg/m³으로서 평균 오차범위가 상대적으로 낮은 범위에 있었다. Cluster 3의 상대오차율 MAPE는 각각 54.93%, 32.57%, 33.76%, 23.40%, 20.64%, 33.26%로서 NO₂의 상대오차율이 다른 지역에 비해 높게 나타났으며, 이러한 결과는 다른 두 지역 대비 NO₂의 농도 범위가 낮은 데서 기인한다.

Fig. 8.

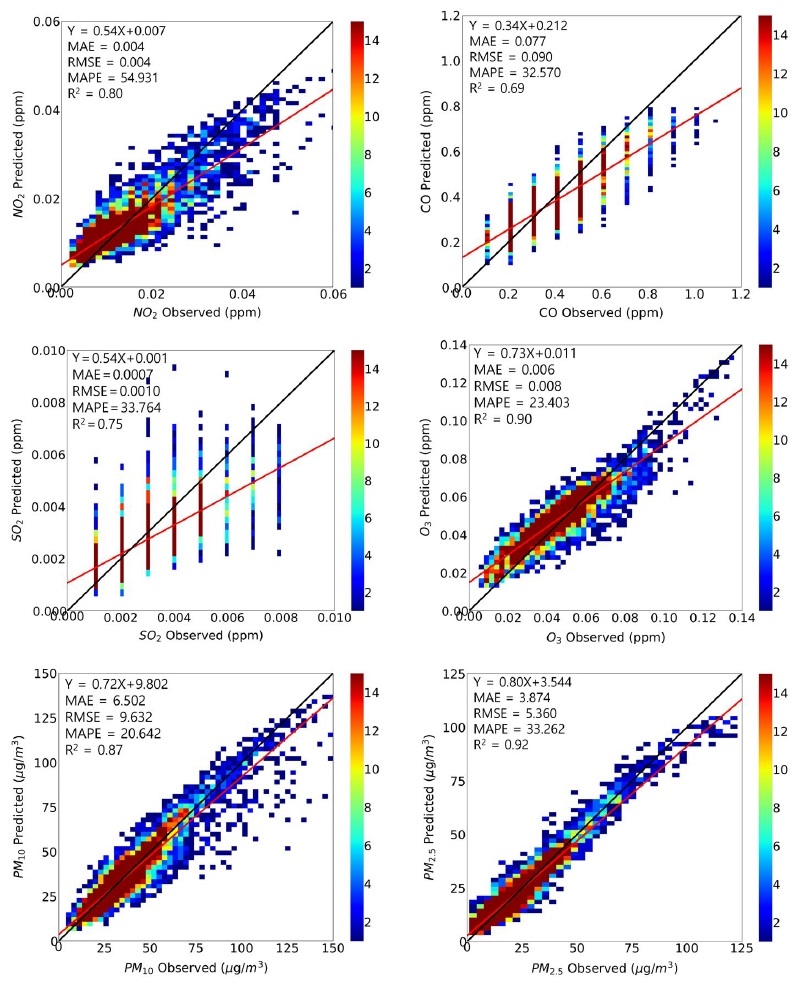
Scatterplots of optimal model prediction and observed air pollutants concentrations for Cluster 3 during a year of 2019.

이상의 결과를 종합하면, 머신러닝 기반의 모델을 이용한 대기질 예측 결과는 실제 관측값과의 비교를 통하여 다음과 같은 오차범위와 정확도를 가지는 것으로 나타났다. NO₂, CO, SO₂, O₃, PM₁₀, PM_2.5의 평균 MAE는 각각 0.004±0.001 ppm, 0.069±0.009 ppm, 0.0006±0.00006 ppm, 0.0006±0.0006 ppm, 5.392±0.961 µg/m³, 3.258±0.575 µg/m³의 범위이며, 상대오차율 MAPE는 각각 31.23±20.54%, 22.03±9.75%, 26.12±9.26%, 27.28±12.74%, 16.53±3.57%, 24.43±8.42%로서 전체 오염물질의 평균적인 오차율은 약 24.60%로 평가되었다.

각 Cluster별 시계열 변화특성을 분석하기 위하여, 그림 9~11에서는 2019년 한 해 동안 1주일의 기간 중 각 시간대별 평균값에 대한 시계열 변화를 나타내었다. 그림 9의 Cluster 1의 경우 대부분의 대기오염물질의 요일별 변화 패턴은 주말로 갈수록 낮아지고 있으나, O₃은 상대적으로 커지고 있는 경향을 보이고 있다. 또한, 일변화에서는 오전과 오후 출퇴근 시간대에 증가하는 NO₂, CO와 정오 근처에서 광화학반응으로 인하여 최대값을 나타내는 O₃의 일반적인 경향을 잘 나타낸다. 그림 10의 Cluster 2에서는 이러한 일변화 특성이 더욱 뚜렷하게 나타나는 것을 확인할 수 있다. 특히 SO₂의 일변화 경향이 더욱 크게 나타나며, 이러한 결과는 해당 지역이 산업단지나 대도시를 포함하고 있어 SO₂ 배출원의 영향이 큰 것으로 판단된다. 또한 이 지역에서의 PM₁₀, PM_2.5의 농도 변화는 평일 야간에 증가하고 있는 추세를 보이고 있으며, 해당 지역에서의 배출원과 기상학적 요인이 복합적으로 작용된 결과로 추정된다.

Fig. 9.

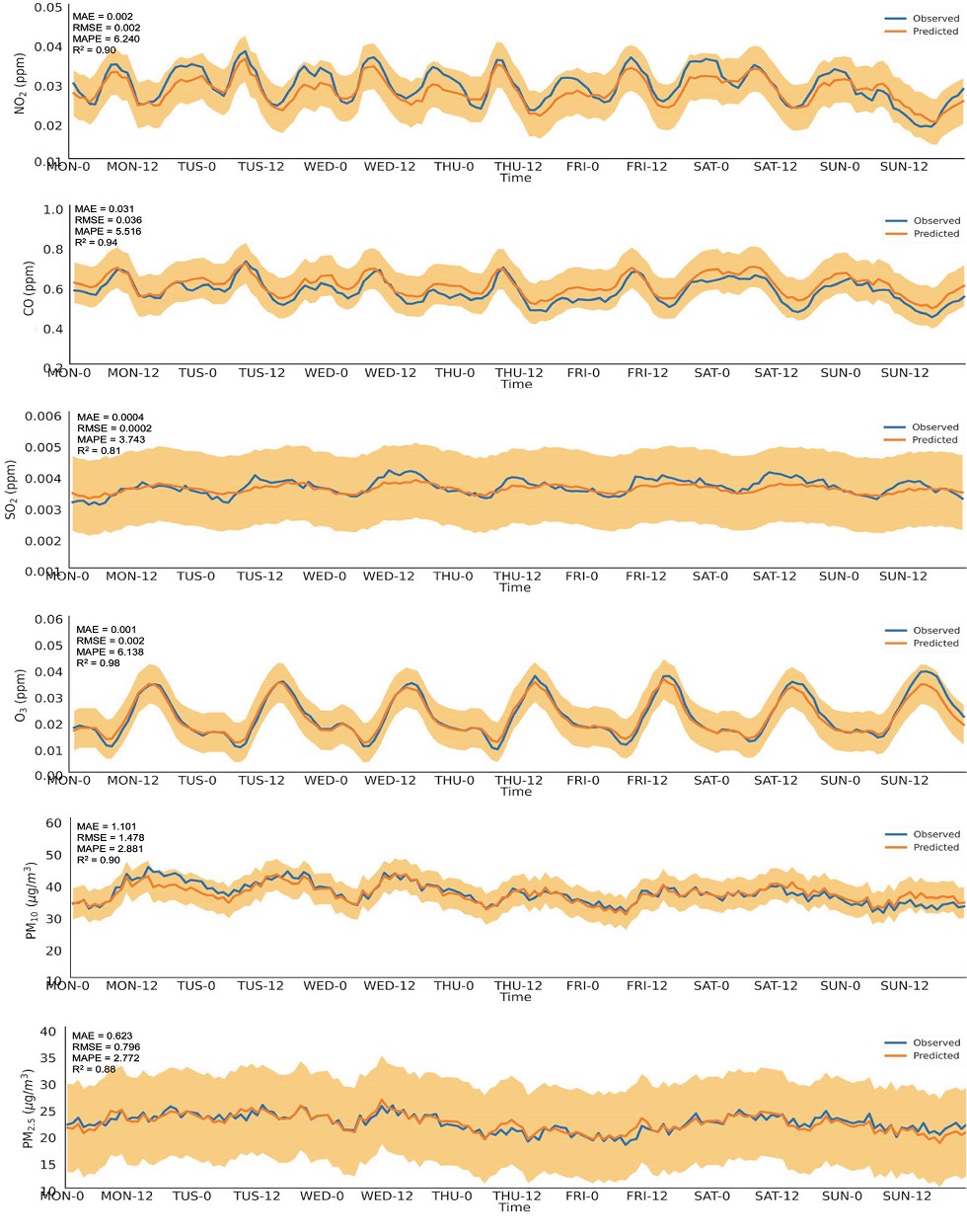
Observed (blue) and predicted (orange) hourly variations of air pollutants concentrations for cluster 1. Shade represent ±RMSE of predicted model.

Fig. 10.

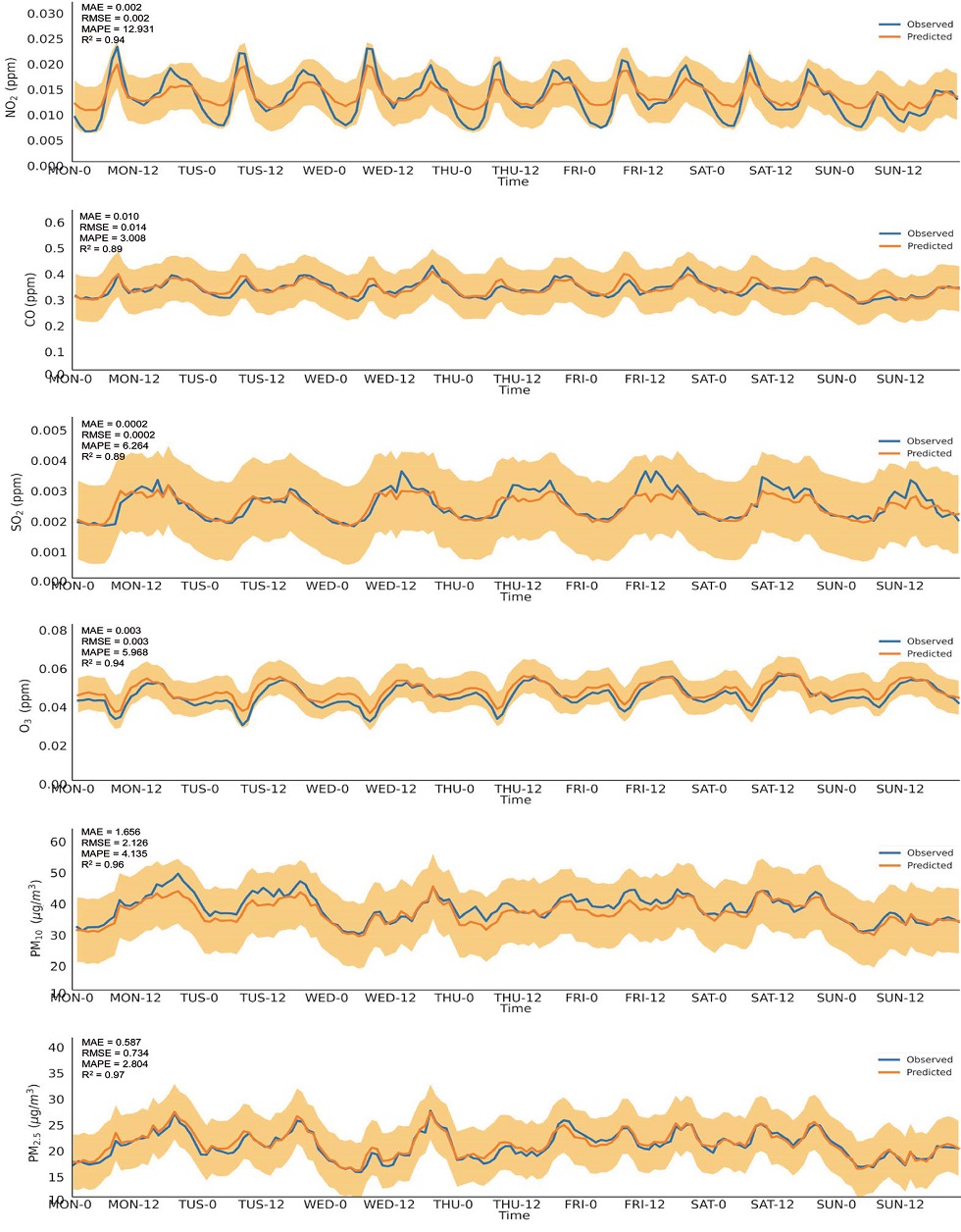
Observed (blue) and predicted (orange) hourly variations of air pollutants concentrations for cluster 2. Shade represent ±RMSE of predicted model.

Fig. 11.

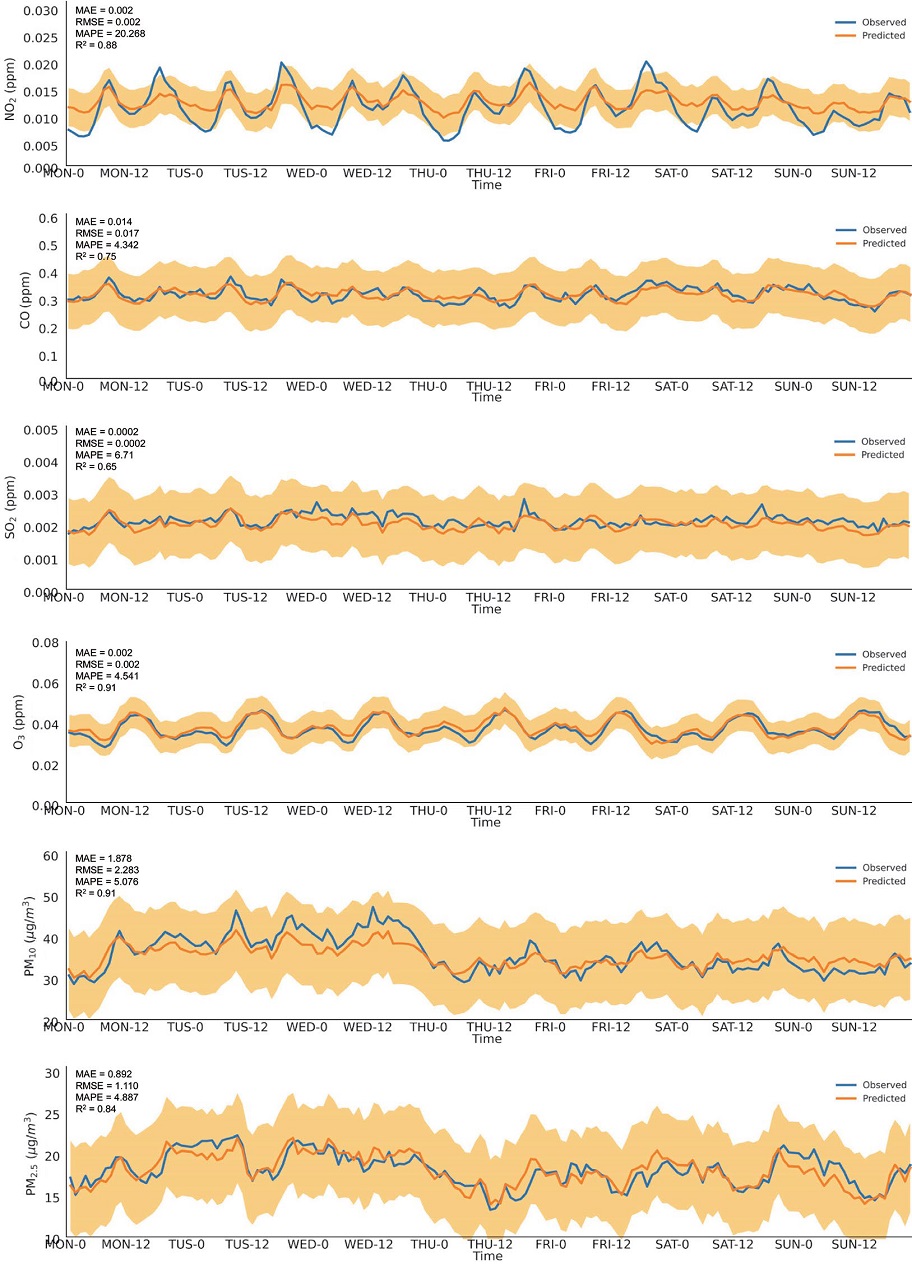
Observed (blue) and predicted (orange) hourly variations of air pollutants concentrations for cluster 3. Shade represent ±RMSE of predicted model.

한편, 그림 9~11의 결과를 통하여 실제 관측값이 최적화 모델을 통하여 예측된 대기오염물질의 농도값의 예상된 오차범위 안에 들어간 경우 (즉, )에 대하여 모델의 예측 적중률을 계산하였다. 2019년 기간 동안 모델로 예측한 NO₂, CO, SO₂, O₃, PM₁₀, PM_2.5의 예측 적중률은 91.2~100%의 범위로서 예측 모델의 성능이 유효함을 입증하였다.

4. 결 론

대기오염은 대부분 국가에서 심각한 환경 문제로 인식하고 있으며, 대기오염에 의한 피해를 최소화하기 위해 대기질 관측과 예보가 매우 중요하다. 본 연구에서는 국내의 10개 도시대기측정망 관측 지점 (강릉시, 광주광역시, 대구광역시, 대전광역시, 목포시, 부산광역시, 서울특별시, 울산광역시, 원주시, 제주시) 및 최근거리의 ASOS 자료를 이용하였다. 획득된 관측 자료는 머신러닝 기법 중 RF, SVM, MLR, DNN에 각각 적용하여 최적의 모델을 선정하였고, 선정된 최적의 모델을 이용하여 대기오염물질의 농도를 예측하고 평가하여 다음과 같은 결론을 도출하였다.

첫째, 획득한 국내 대기질 관측 자료와 기상관측 자료의 특성을 분류하기 위해 머신러닝 클러스터링 기법을 적용한 결과는 3개의 주요 Cluster로 분류하는 것이 이상적이며, 개별 클러스터는 Cluster 1 (서울), Cluster 2 (제주, 부산, 원주, 대전, 대구, 울산, 광주, 목포), Cluster 3 (강릉)으로 분류되었다. 대기오염물질의 농도는 O₃을 제외하고 Cluster 1 관측 지점에서 제일 높은 수준을 나타냈으며, 반대로 Cluster 2의 경우는 O₃을 제외한 대기오염물질의 농도가 제일 낮은 수준을 보였다. Cluster 1, 2의 풍향이 주로 남풍계열인 것과는 다르게 Cluster 3은 서풍 계열의 바람과 Cluster 2보다 상대적으로 높은 대기오염물질의 농도가 나타났다.

둘째, 개별 Cluster에 대하여 RF, SVM, MLR, DNN 기법에 적용한 결과는 입력자료별 모델의 정확도가 모두 다른 결과를 나타내므로, 개별 훈련된 모델의 정확도 테스트를 통하여 개별 검증지수 등급에 대한 평가를 통해 최적 모델을 선정하였다. 이러한 과정에서 결정된 최적의 예측 모델은 대기오염물질의 농도 예측에 정확도를 높일 수 있었다.

셋째, 앞서 선정된 최적의 모델을 이용하여 2019년 한 해 기간 동안의 대기질 예측에 적용하여 예측한 값과 실제 관측값과의 비교검증 결과는 NO₂, CO, SO₂, O₃, PM₁₀, PM_2.5에 대한 평균 MAE는 각각 0.004±0.001 ppm, 0.069±0.009 ppm, 0.0006±0.00006 ppm, 0.0006±0.0006 ppm, 5.392±0.961 µg/m³, 3.258±0.575 µg/m³의 범위이며, 상대오차율 MAPE는 각각 31.23±20.54%, 22.03±9.75%, 26.12±9.26%, 27.28±12.74%, 16.53±3.57%, 24.43±8.42%로서 전체 오염물질의 평균적인 오차율은 약 24.60%로 정확도는 75.40%로 평가되었다. 또한, 예측 모델의 오차범위 안에 관측값이 위치하는 예측 적중률은 91.2~100%의 범위로서 예측 모델의 성능이 유효함을 입증하였다.

본 연구의 방법론과 결과를 통해 국내 대기질 특성에 따른 정밀한 예측이 가능하게 함으로써, 대기오염물질 농도 예측 모델의 검증과 보조자료로 활용할 수 있을 것으로 판단된다.

Acknowledgments

이 논문은 2019년도 정부 (교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(NRF^-2019R1I1A3A01062804).

References

• Ahmad, A., Dey, L. (2007) A K-mean Clustering Algorithm for Mixed Numeric and Categorical Data, Data & Knowledge Engineering, 63(2), 503-527. [https://doi.org/10.1016/j.datak.2007.03.016]
• Breiman, L. (2001) Random Forests, Machine Learning, 45(1), 5-32. [https://doi.org/10.1023/A:1010933404324]
• Castelli, M., Clemente, F.M., Popovič, A., Silva, S., Vanneschi, L. (2020) A Machine Learning Approach to Predict Air Quality in California, Complexity, 2020, 8049504. [https://doi.org/10.1155/2020/8049504]
• Charrad, M., Chazzali, N., Boiteau, V., Niknafs, A. (2014) NbClust: An R Package for Determining the Relevant Number of Clusters in A Data Set, Journal of Statistical Software, 61(6), 1-36. [https://doi.org/10.18637/jss.v061.i06]
• Cho, K.-H., Lee, B.-Y., Kwon, H.-M., Kim, S.-C. (2019) Air Quality Prediction Using a Deep Neural Network Model, Journal of Korean Society for Atmospheric Environment, 35(2), 214-225, (in Korean with English abstract). [https://doi.org/10.5572/KOSAE.2019.35.2.214]
• Choi, D.-R., Yun, H.-Y., Koo, Y.-S. (2019) A Development of Air Quality Forecasting System with Data Assimilation using Surface Measurements in East Asia, Journal of Korean Society for Atmospheric Environment, 35(1), 60-85, (in Korean with English abstract). [https://doi.org/10.5572/KOSAE.2019.35.1.060]
• Choi, J.-H., Seo, D.S. (1999) Decision Trees and its Applications, Journal of The Korean Official Statistics, 4(1), 61-83.
• Cortes, C., Vapnik, V. (1995) Support-Vector Networks, Machine Learning, 20, 273-297. [https://doi.org/10.1007/BF00994018]
• Goyal, P., Chan, A.-T., Jaiswal, N. (2006) Statistical Models for the Prediction of Respirable Suspended Particulate Matter in Urban Cities, Atmospheric Environment, 40(11), 2068-2077. [https://doi.org/10.1016/j.atmosenv.2005.11.041]
• Günther, F., Fritsch, S. (2010) Neuralnet: training of neural networks, The R Journal, 2(1), 30-38. [https://doi.org/10.32614/RJ-2010-006]
• Hearst, M.-A., Dumais, S.-T., Osman, E., Platt, J., Scholkopf, B. (1998) Trends and Controversies: Support Vector Machines, IEEE Intelligent System, 13(4), 18-28. [https://doi.org/10.1109/5254.708428]
• Hooyberghs, J., Mensink, C., Dumont, G., Fierens, F., Brasseur, O. (2005) A Neural Network Forecast for Daily Average PM₁₀ Concentrations in Belgium, Atmospheric Environment, 39(18), 3279-3289. [https://doi.org/10.1016/j.atmosenv.2005.01.050]
• Hrust, L., Klaić, Z.-B., Križan, J., Antonić, O., Hercog, P. (2009) Neural Network Forecasting of Air Pollutants Hourly Concentrations Using Optimised Temporal Averages of Meteorological Variables and Pollutant Concentrations, Atmospheric Environment, 43(35), 5588-5596. [https://doi.org/10.1016/j.atmosenv.2009.07.048]
• Jang, D.-H. (2020) Applications of R Package for Statistical Engineering, The Korean Journal of Applied Statistics, 33(1), 87-105, (in Korean with English abstract).
• Kim, D.-H., Hwang, K.-Y., Yoon, Y. (2019) Prediction of Traffic Congestion in Seoul by Deep Neural Network, The Journal of the Korea Institute of Intelligent Transport Systems, 18(4), 44-57, (in Korean with English abstract). [https://doi.org/10.12815/kits.2019.18.4.44]
• Kim, M.-W., Jeong, H.-S. (2022a) Development of Machine Learning Based Prediction of Particulate Matter Concentration in Seoul, Journal of the Korean Data & Information Science Society, 33(6), 1095-1111. [https://doi.org/10.7465/jkdi.2022.33.6.1095]
• Kim, Y.-I., Lee, K.-H., Lee, K.-T. (2022b) Evaluation and Prediction of Column Aerosol by Using the Time Series Machine Learning Technique, Journal of Korean Society for Atmospheric, Environment, 38(1), 57-73, (in Korean with English abstract). [https://doi.org/10.5572/KOSAE.2022.38.1.57]
• Korean Institute of Environmental Science and Technology (KIEST) (2007) A Development of Air Quality Forecasting System.
• LeCun, Y., Boser, B., Denker, J., Henderson, D., Howard, R., Hubbard, W., Jackel, L. (1989) Handwritten Digit Recognition with a Back-Propagation Network, Advances in Neural Information Processing Systems, 2.
• Lee, M.-J., Lee, S.-R., Jeon, S.-W. (2012) Landslide Hazard Mapping and Verification Using Probability Rainfall and Artificial Neural Networks, Journal of the Korean Association of Geographic Information Studies 15(2), 57-70, (in Korean with English abstract). [https://doi.org/10.11108/kagis.2012.15.2.057]
• National Institute of Environmental Research (NIER) (2021) Air Environment Annual Report.
• Oh, I.-B., Bang, J.-H., Kim, S.-T., Kim, E.-H., Hwang, M.-K., Kim, Y.-H. (2016) Spatial Distribution of Air Pollution in the Ulsan Metropolitan Region, Journal of Korean Society for Atmospheric Environment, 32(4), 394-407, (in Korean with English abstract). [https://doi.org/10.5572/KOSAE.2016.32.4.394]
• Pyo, S.-H., Lee, K.-H., Lee, K.-T. (2021) Estimation of Column Aerosol Contribution in Seoul and Gangneung Using Machine Learning Clustering Technique, Journal of Korean Society for Atmospheric, Environment, 37(6), 931-945, (in Korean with English abstract). [https://doi.org/10.5572/KOSAE.2021.37.6.931]
• Pyo, S.-H., Lee, K.-H. (2022) Estimation of Aerosol Radiative Forcing Using Deep Learning Technique, Journal of Korean Society for Atmospheric, Environment, 38(5), 669-686, (in Korean with English abstract), [https://doi.org/10.5572/KOSAE.2022.38.5.669]
• Shin, D.-C. (2007) Health Effects of Ambient Particulate Matter, Journal of Korean Med Association, 50(2), 175-182, (in Korean with English abstract). [https://doi.org/10.5124/jkma.2007.50.2.175]
• World Health Organization (WHO) (2014) 7 million premature deaths annually linked to air pollution. https://www.who.int/news/item/25-03-2014-7-million-premature-deaths-annually-linked-to-air-pollution